树型数据结构

这四种树分别是Segment Tree（线段树）、Interval Tree（间隔树）、Range Tree（范围树）、Binary Indexed Tree（二叉索引树）。

严格上来说，BIT不算树，事实上是将根据数字的二进制表示来对数组中的元素进行逻辑上的分层存储。

使用场景

• Segment tree stores intervals, and optimized for "which of these intervals contains a given point" queries.

• Interval tree stores intervals as well, but optimized for "which of these intervals overlap with a given interval" queries. It can also be used for point queries - similar to segment tree.

• Range tree stores points, and optimized for "which points fall within a given interval" queries.

• Binary indexed tree stores items-count per index, and optimized for "how many items are there between index m and n" queries.

  k is the number of reported results.

时间复杂度

One Dimension

Operation	Segment	Interval	Range	Indexed
Preprocessing	$n\log n$	$n\log n$	$n\log n$	$n\log n$
Query	$k+\log n$	$k+\log n$	$k+\log n$	$\log n$
Space	$n\log n$	$n$	$n$	$n$
Insert/Delete	$\log n$	$\log n$	$\log n$	$\log n$

Higher Dimensions ($d>1$)

Operation	Segment	Interval	Range	Indexed
Preprocessing	$n(\log n{)}^d$	$n\log n$	$n(\log n{)}^d$	$n(\log n{)}^d$
Query	$k+(\log n{)}^d$	$k+(\log n{)}^d$	$k+(\log n{)}^d$	$(\log n{)}^d$
Space	$n(\log n{)}^{d-1}$	$n\log n$	$n(\log n{)}^{d-1}$	$n(\log n{)}^d$

注：以上内容来自Stack Overflow并经过了本人的认真阅读。在对比了国内外的大部分参考资料后， 决定以国外的英文讲解为主，中文的内容由于翻译等的错误和不妥，将不会排至首位使用，除非在经过仔细核对后。

参考资料

1. algorithm - Are interval, segment, fenwick trees the same? - Stack Overflow
2. algorithm - What are the differences between segment trees, interval trees, binary indexed trees and range trees? - Stack Overflow
3. Interval tree - Wikipedia
4. Segment tree - Wikipedia
5. Range tree - Wikipedia
6. Fenwick tree - Wikipedia
7. Multi-dimensional Dynamic Ranged Tree Based On An AVL Tree
8. 树状数组 - OI Wiki (oi-wiki.org)
9. 线段树 - OI Wiki (oi-wiki.org)

Fenwick Tree

Fenwick树的简介

1. Fenwick树（二叉索引树、树状数组）是一种数据结构，用于有效地计算数字序列（数组）的前缀和。它也被称为芬威克树，因为彼得·芬威克通过他的论文将其介绍给世界。

2. Fenwick树虽然名字叫二叉索引树，但是，它不算是一棵二叉树。

3. 树状数组是一种支持 单点修改 和 区间查询 的，代码量小的数据结构。普通树状数组维护的信息及运算要满足 结合律 且 可差分，如加法（和）、乘法（积）、异或等。

   • 模意义下的乘法若要可差分，需保证每个数都存在逆元（模数为质数时一定存在）；
   • 例如 $gcd,max$ 这些信息不可差分，所以不能用普通树状数组处理，但是，使用两个树状数组可以用于处理区间最值。

4. 事实上，树状数组能解决的问题是线段树能解决的问题的子集：树状数组能做的，线段树一定能做；线段树能做的，树状数组不一定可以。然而，树状数组的代码要远比线段树短，时间效率常数也更小，因此仍有学习价值。有时候，在差分数组和辅助数组的帮助下，树状数组还可以解决更强的 区间加端点值 和 区间加区间和 的问题。

Fenwick树

初步认识

1. 例子：求$a[1,\dots ,7]$ 的前缀和。我们可以将数组中的每一项相加作为最终的答案。但，如果已知三个数 $A,B,C$，且$A=a[1\dots 4]$ 的和，$B=a[5\dots 6]$ 的总和，$C=a[7\dots 7]$ 的总和（其实就是 $a[7]$ 自己），我们就会直接把 A,B,C 相加，作为我们的和。这就是树状数组何以快速求解信息的原因：我们总能将一段前缀 $[1,n]$ 拆成 不多于 $\log n$ 段区间，使得这 $\log n$ 段区间的信息是 已知的。所以，合并这$\log n$段信息就能得到答案。相较于原来的直接合并 $n$ 个信息，效率有了很大的提高。

2. 树状数组的工作原理如下，其中，$c[x]$ 管辖的一定是一段右边界是 $x$ 的区间总信息。

3. 例子：计算 $a[4\dots 7]$ 的和。我们是从 $c_7$ 开始跳，跳到 $c_6$ 再跳到 $c_4$。此时我们发现它管理了 $a[1\dots 4]$ 的和，但是我们不想要 $a[1\dots 3]$ 这一部分，怎么办呢？很简单，减去 $a[1\dots 3]$ 的和就行了。那不妨考虑最开始，就将查询 $a[4\dots 7]$ 的和转化为查询 $a[1\dots 7]$ 的和，以及查询 $a[1\dots 3]$ 的和，最终将两个结果作差。这就是树状数组的查询过程。

管辖区间

一个节点 $c[x]$ 管辖的区间是 $[x-lowbit(x)+1,x]$。其中，$lowbit(x)=x\mathrm{\&}-x$。

树状数组中，规定 $c[x]$ 管辖的区间长度为 $2^k$，其中：

• 设二进制最低位为第 $0$ 位，则 $k$ 恰好为 $x$ 二进制表示中，最低位的 1 所在的二进制位数；
• $2^k$（$c[x]$ 的管辖区间长度）恰好为 $x$ 二进制表示中，最低位的 1 以及后面所有 0 组成的数。
• 这里注意：$lowbit$ 指的不是最低位 1 所在的位数 $k$，而是这个 1 和后面所有 0 组成的 $2^k$。

• lowbit的原理：

• 设原先 x 的二进制编码是 (...)10...00，全部取反后得到 [...]01...11，加 1 后得到 [...]10...00，也就是 -x 的二进制编码了。这里 x 二进制表示中第一个 1 是 x 最低位的 1。

(...) 和 [...] 中省略号的每一位分别相反，所以 x & -x = (...)10...00 & [...]10...00 = 10...00，得到的结果就是 lowbit。

区间查询

1. 其实任何一个区间查询都可以这么做：查询 $a[l\dots r]$ 的和，就是 $a[1\dots r]$ 的和减去 $a[1\dots l-1]$ 的和，从而把区间问题转化为前缀问题，更方便处理。事实上，将有关 $l\dots r$ 的区间询问转化为 $1\dots r$ 和 $1\dots l-1$ 的前缀询问再差分，在竞赛中是一个非常常用的技巧。

2. 前缀查询：查询 $a[1\dots x]$ 的和的过程如下：

   • 从 $c[x]$ 开始往前跳，有 $c[x]$ 管辖 $a[x-\text{lowbit}(x)+1\dots x]$；
   • 令 $x\leftarrow x-\text{lowbit}(x)$，如果 $x=0$ 说明已经跳到尽头了，终止循环；否则回到第一步。
   • 将跳到的 $c$ 合并。

   实现时，我们不一定要先把 $c$ 都跳出来然后一起合并，可以边跳边合并。

树状数组与其树形态的性质

1. 我们约定：

   1. $l(x)=x-\text{lowbit}(x)+1$。即，$l(x)$ 是 $c[x]$ 管辖范围的左端点。
   2. 对于任意正整数 $x$，总能将 $x$ 表示成 $s\times 2^{k+1}+2^k$ 的形式，其中 $lowbit(x)=2^k$。
   3. 下面「$c[x]$ 和 $c[y]$ 不交」指 $c[x]$ 的管辖范围和 $c[y]$ 的管辖范围不相交，即 $[l(x),x]$ 和 $[l(y),y]$ 不相交。「$c[x]$ 包含于 $c[y]$」等表述同理。

2. 性质1：对于$x\le y$，要么$c[x]$ 和 $c[y]$ 不交，要么$c[x]$ 包含于 $c[y]$。

证明：设 $x=s\times 2^{k+1}+2^k$，$y=t\times 2^{l+1}+2^l$，其中 $s,t$ 为非负整数，$k,l$ 为非负整数。不妨设 $k\le l$。

• 若 $k=l$，则 $x=y$，显然不交。
• 若 $k<l$，则 $x\le y-2^l<y$，即 $c[x]$ 包含于 $c[y]$。

3. 性质2：$c[x]$真包含于$c[y]$当且仅当$x=y-\text{lowbit}(y)$。

证明：$c[x]$ 包含于 $c[y]$，则 $l(y)\le l(x)\le x\le y$，即 $l(y)=x$。反之，若 $x=y-\text{lowbit}(y)$，则 $l(y)=y-\text{lowbit}(y)+1=x$，即 $c[x]$ 包含于 $c[y]$。

4. 性质3：对于任意$x<y<x+\text{lowbit}(x)$，有$c[x]$和$c[y]$不交。

证明：设$x=s\times 2^{k+1}+2^k$，$y=t\times 2^{l+1}+2^l$，其中$s,t$为非负整数，$k,l$为非负整数。不妨设$k\le l$。

• 若$k=l$，则$x=y$，显然不交。
• 若$k<l$，则$x<y-2^l<x+2^k$，即$c[x]$和$c[y]$不交。

5. 观察树状数组的形态：对于上图来说，忽略a向c的连边，树状数组的形态是$x$向$x+\text{lowbit}(x)$连边得到的图，其中 $x+\text{lowbit}(x)$ 是 $x$ 的父亲。这棵可以认为是无限大的树有很多好的性质：

• $u<fa[u]$。
• $u$ 大于任何一个 $u$ 的后代，小于任何一个 $u$ 的祖先。
• 点 $u$ 的 $\text{lowbit}$ 严格小于 $fa[u]$ 的 $\text{lowbit}$。
• $c[u]$ 真包含于 $c[fa[u]]$（性质 $2$）。
• $c[u]$ 真包含于 $c[v]$，其中 $v$ 是 $u$ 的任一祖先（在上一条性质上归纳）。
• $c[u]$ 真包含 $c[v]$，其中 $v$ 是 $u$ 的任一后代（上面那条性质 $u$，$v$ 颠倒）。
• 对于任意 $v^{\prime }>u$，若 $v^{\prime }$ 不是 $u$ 的祖先，则 $c[u]$ 和 $c[v^{\prime }]$ 不交。
• 对于任意 $v<u$，如果 $v$ 不在 $u$ 的子树上，则 $c[u]$ 和 $c[v]$ 不交（上面那条性质 $u$，$v^{\prime }$ 颠倒）。
• 对于任意 $v>u$，当且仅当 $v$ 是 $u$ 的祖先，$c[u]$ 真包含于 $c[v]$（上面几条性质的总结）。这就是树状数组单点修改的核心原理。
• 设 $u=s\times 2^{k+1}+2^k$，则其儿子数量为 $k={\log }_2\text{lowbit}(u)$，编号分别为 $u-2^t(0\le t<k)$。
• $u$的所有儿子对应的管辖区间恰好拼接成$[l(u),u-1]$。

单点修改

区间加区间和

参考文献

1. Fenwick, P. M. . (2010). A new data structure for cumulative frequency tables. Soft.pract.exp, 24(3), 327-336.

Interval Tree 区间树

从Stabbing Query问题开始

问题描述：在一维的情况下，给出一组区间$S=\{s_i=[x_i,x_i^{\prime }]\mid 1\le x\le n\}$，和一个点$q_x$。现在，请你找出所有包含点$q_x$的区间。这个问题称为窗口问题/截窗问题，适合用区间树来求解。

区间树

1. 定义：区间树是用于保存区间的树数据结构。具体来说，它允许人们有效地找到与任何给定区间或点重叠的所有区间。

2. Definition: An interval tree is a tree data structure to hold intervals. Specifically, it allows one to efficiently find all intervals that overlap with any given interval or point.

3. 区间树的部分特点/性质：建树的时间复杂度为$O(n\log n)$，空间复杂度为$O(n)$；有效地插入/删除区间的时间复杂度为$O(\log n)$，若运行时间(Runtime)为$m$，则搜索的时间复杂度为$O(\log n+m)$。

4. 特别地，如果区间的右端点在一个非常小的整数集之间，（如：$1,2,\dots ,O(n)$）则我们甚至可以使用改良版的“间隔树”来实现这一个预处理的时间复杂度为$O(n)$，查询的时间复杂度为$O(1+m)$的算法。(Schmidt, 2009)

Stabbing Query的解法

1. 若区间不相重叠，则完全可以使用一棵普通的BST存储所有的区间，此时的时间复杂度在$O(\log n)$。

2. 但是，对于有重叠的区间，因为左、右端点的相对情况未知，所以不能使用上述方法。或许，我们可以使用两棵BST分别存放左、右端点。但是，因为合并结果并找出答案需要$O(\log n+n)=O(n)$的时间，时间复杂度不尽人意。这时，我们就应该使用区间树了。Wikipedia介绍了区间树的两种备选设计，称为居中区间树和增强树。

3. 居中区间树(Centered Interval Tree)：

4. 令点集$P$为所有区间的左、右端点。（$\text{Card}(A)=2n$）再令$x_{mid}$为点集$P$的中间元素。

5. 现在，所有区间可以被划分成3个子集合：$S_{Left}=\{S_i|x_i^{\prime }<x_{mid}\}$、$S_{Mid}=\{S_i|x_i\le x_{mid}\le x_i^{\prime }\}$和$S_{Right}=\{S_i|x_i>x_{mid}\}$。我们可以递归地构建区间树，直到区间的个数为1。这里，我们有：

$$max(\text{Card}(S_L),\text{Card}(S_R))\le \frac{n}{2}$$$$\text{Best Case: }\text{Card}(S_{Mid})=n,\text{Worst Case: }\text{Card}(S_{Mid})=1$$

​

3. 观察：只要不含点$x_{mid}$的区间就会被归为左/右子集合，而包含的（含端点）则会被划分至中间的子集合。同时，令$L_{L/R}$为所有按照左/右端点排列的在中间子集的区间元素。所以，所有的区间会出现两次。（即在以左、右端点为代表的区间集$L_L,L_R$各出现一次）

4. 建立二叉树：现在，可以建立一棵二叉树，其中，每个节点应该存储：

• 中心点
• 指向另一个节点的指针，该节点包含中心点左侧的所有间隔
• 指向另一个节点的指针，该节点包含完全位于中心点右侧的所有间隔
• 所有与中心点重叠的间隔，按其起点排序
• 与中心点重叠的所有间隔，按其终点排序

• Center point
• Pointer to another node containing all intervals completely to the Left/Right of the center point
• All intervals overlapping the center point sorted by their Beginning/Ending point

5. 进行查找$q_x$：代码如下。对于这个线性递归，每一次查询需要访问$O(\log n+m)$个节点。

void queryIntervalTree(int xmid(v), int qx){
    if(!v) return;//base
    if(qx<xmid(v)){
        use L-list to report all intervals of Smid(v) containing qx;
        queryIntervalTree(lc(v),qx);
    }
    else if (xmid(v)<qx){
        use R-list to report all intervals of Smid(v) containing qx;
        queryIntervalTree(rc(v),qx);
    }
    else{
        report all segments of Smid(v);
        //ignore rc(v) and lc(v), since has been found.
    }
}

增强树(Augmented Tree)

参考资料

1. Schmidt, Jens. (2009). Interval Stabbing Problems in Small Integer Ranges. Lecture Notes in Computer Science. 5878. 163-172. 10.1007/978-3-642-10631-6_18. https://dx.doi.org/10.1007/978-3-642-10631-6_18
2. 间隔树 - 维基百科，自由的百科全书 (wikipedia.org)
3. DSACPP | 清华大学(tsinghua.edu.cn)

稀疏表(ST表)

简介

• 稀疏表(Sparse Table, ST)是一种用于解决可重复贡献问题(通常是区间查询问题)的数据结构，可以在$O(1)$的时间内回答区间最值查询问题。
• 可重复贡献问题：是指对于运算$\oplus$，满足$x\oplus x=x$，则对应的区间询问就是一个可重复贡献问题，如求最大值的$max(x,x)=x$和求最大公约数的$gcd(x,x)=x$。所以，RMQ（求区间的最值）问题和求区间的最大公约数问题就是可重复贡献问题。
  • 另外，不是所有的可重复贡献问题都可以使用ST表解决，运算符$\oplus$必须满足结合律才可以使用ST表求解。

引入

求区间最大值问题：给定一个长度为$n$的序列$a$，一共有$m$次询问，对于每个询问$(l,r)$，求$a[l,r]$的最大值。

• 对于直接求解的方法，时间复杂度为$O(nm)$，对于较大的$n$和$m$，这种方法是不可接受的。
• 或许，我们可以试试ST表，其时间复杂度为$O(n\log n+m)$。

ST表

ST 表基于倍增思想，可以做到 $\mathrm{\Theta }(n\log n)$ 预处理，$\mathrm{\Theta }(1)$ 回答每个询问。但是不支持修改操作。

基于倍增思想，我们考虑如何求出区间最大值。可以发现，如果按照一般的倍增流程，每次跳 $2^i$ 步的话，询问时的复杂度仍旧是 $\mathrm{\Theta }(\log n)$，并没有比线段树更优，反而预处理一步还比线段树慢。

我们发现 $max(x,x)=x$，也就是说，区间最大值是一个具有「可重复贡献」性质的问题。即使用来求解的预处理区间有重叠部分，只要这些区间的并是所求的区间，最终计算出的答案就是正确的。

如果手动模拟一下，可以发现我们能使用至多两个预处理过的区间来覆盖询问区间，也就是说询问时的时间复杂度可以被降至 $\mathrm{\Theta }(1)$，在处理有大量询问的题目时十分有效。（分治、动态规划）

具体实现如下：

（预处理）

• 令 $f(i,j)$ 表示区间 $[i,i+2^j-1]$ 的最大值，显然 $f(i,0)=a_i$。

  根据定义式，第二维就相当于倍增的时候「跳了 $2^j-1$ 步」，依据倍增的思路，写出状态转移方程：$f(i,j)=max(f(i,j-1),f(i+2^{j-1},j-1))$。

  

（查询）

• 对于每个询问 $[l,r]$，我们把它分成两部分：$[l,l+2^s-1]$ 与 $[r-2^s+1,r]$，其中 $s=\lfloor {\log }_2(r-l+1)\rfloor$。两部分的结果的最大值就是回答。

  

（总结）

• 根据上面对于「可重复贡献问题」的论证，由于最大值是「可重复贡献问题」，重叠并不会对区间最大值产生影响。又因为这两个区间完全覆盖了 $[l,r]$，可以保证答案的正确性。

代码实现

C语言风格

#include <bits/stdc++.h>
using namespace std;
const int logn = 21;
const int maxn = 2000001;
int f[maxn][logn + 1], Logn[maxn + 1];

int read() {  // 快读
  char c = getchar();
  int x = 0, f = 1;
  while (c < '0' || c > '9') {
    if (c == '-') f = -1;
    c = getchar();
  }
  while (c >= '0' && c <= '9') {
    x = x * 10 + c - '0';
    c = getchar();
  }
  return x * f;
}

void pre() {  // 准备工作，初始化
  Logn[1] = 0;
  Logn[2] = 1;
  for (int i = 3; i < maxn; i++) {
    Logn[i] = Logn[i / 2] + 1;
  }
}

int main() {
  int n = read(), m = read();
  for (int i = 1; i <= n; i++) f[i][0] = read();
  pre();
  for (int j = 1; j <= logn; j++)
    for (int i = 1; i + (1 << j) - 1 <= n; i++)
      f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);  // ST表具体实现
  for (int i = 1; i <= m; i++) {
    int x = read(), y = read();
    int s = Logn[y - x + 1];
    printf("%d\n", max(f[x][s], f[y - (1 << s) + 1][s]));
  }
  return 0;
}

C++语言风格

#include <bits/stdc++.h>
using namespace std;

template <typename T>
class SparseTable {
  using VT = vector<T>;
  using VVT = vector<VT>;
  using func_type = function<T(const T &, const T &)>;

  VVT ST;

  static T default_func(const T &t1, const T &t2) { return max(t1, t2); }

  func_type op;

 public:
  SparseTable(const vector<T> &v, func_type _func = default_func) {
    op = _func;
    int len = v.size(), l1 = ceil(log2(len)) + 1;
    ST.assign(len, VT(l1, 0));
    for (int i = 0; i < len; ++i) {
      ST[i][0] = v[i];
    }
    for (int j = 1; j < l1; ++j) {
      int pj = (1 << (j - 1));
      for (int i = 0; i + pj < len; ++i) {
        ST[i][j] = op(ST[i][j - 1], ST[i + (1 << (j - 1))][j - 1]);
      }
    }
  }

  T query(int l, int r) {
    int lt = r - l + 1;
    int q = floor(log2(lt));
    return op(ST[l][q], ST[r - (1 << q) + 1][q]);
  }
};

注意点

1. 输入输出数据一般很多，建议开启输入输出优化。

2. 每次用 std::log 重新计算 log 函数值并不值得，建议进行如下的预处理：

$$\{\begin{array}{l}\mathtt{\text{Logn}}[1]\leftarrow 0,\\ \mathtt{\text{Logn}}\left[i\right]\leftarrow \mathtt{\text{Logn}}\left[\frac{i}{2}\right]+1.\end{array}$$

ST 表维护其他信息

除 RMQ 以外，还有其它的「可重复贡献问题」。例如「区间按位与」、「区间按位或」、「区间 GCD」，ST 表都能高效地解决。

需要注意的是，对于「区间 GCD」，ST 表的查询复杂度并没有比线段树更优（令值域为 $w$，ST 表的查询复杂度为 $\mathrm{\Theta }(\log w)$，而线段树为 $\mathrm{\Theta }(\log n+\log w)$，且值域一般是大于 $n$ 的），但是 ST 表的预处理复杂度也没有比线段树更劣，而编程复杂度方面 ST 表比线段树简单很多。

如果分析一下，「可重复贡献问题」一般都带有某种类似 RMQ 的成分。例如「区间按位与」就是每一位取最小值，而「区间 GCD」则是每一个质因数的指数取最小值。

总结

ST 表能较好的维护「可重复贡献」的区间信息（同时也应满足结合律），时间复杂度较低，代码量相对其他算法很小。但是，ST 表能维护的信息非常有限，不能较好地扩展，并且不支持修改操作。

附录：ST 表求区间 GCD 的时间复杂度分析

在算法运行的时候，可能要经过 $\mathrm{\Theta }(\log n)$ 次迭代。每一次迭代都可能会使用 GCD 函数进行递归，令值域为 $w$，GCD 函数的时间复杂度最高是 $\mathrm{\Omega }(\log w)$ 的，所以总时间复杂度看似有 $O(n\log n\log w)$。

但是，在 GCD 的过程中，每一次递归（除最后一次递归之外）都会使数列中的某个数至少减半，而数列中的数最多减半的次数为 ${\log }_2(w^n)=\mathrm{\Theta }(n\log w)$，所以，GCD 的递归部分最多只会运行 $O(n\log w)$ 次。再加上循环部分（以及最后一层递归）的 $\mathrm{\Theta }(n\log n)$，最终时间复杂度则是 $O(n(\log w+\log x))$，由于可以构造数据使得时间复杂度为 $\mathrm{\Omega }(n(\log w+\log x))$，所以最终的时间复杂度即为 $\mathrm{\Theta }(n(\log w+\log x))$。

而查询部分的时间复杂度很好分析，考虑最劣情况，即每次询问都询问最劣的一对数，时间复杂度为 $\mathrm{\Theta }(\log w)$。因此，ST 表维护「区间 GCD」的时间复杂度为预处理 $\mathrm{\Theta }(n(\log n+\log w))$，单次查询 $\mathrm{\Theta }(\log w)$。

线段树的相应操作是预处理 $\mathrm{\Theta }(n\log x)$，查询 $\mathrm{\Theta }(n(\log n+\log x))$。

更加详细的分析可以参考附录：ST表求区间Gcd的时间复杂度分析

参考资料

ST 表 - OI Wiki (oi-wiki.org)

并查集

引入

• 概念：并查集是一种描述不相交集合的树型的数据结构，即若一个问题涉及多个元素，它们可划归到不同集合，同属一个集合内的元素等价，不同集合内的元素不等价。并查集可以用来处理一些不相交集合的合并和查询问题。

• 主要构成：并查集主要又一个森林和两种主要方法构成。

  • 森林：并查集是一种树状的可能不相交集合的结构，因此需要一个森林，其中， 其中每棵树表示一个集合，树中的节点表示对应集合中的元素。
  • 主要方法1：合并(Union)：合并两个元素所属集合（合并对应的树）
  • 主要方法2：查询(Find)：查询某个元素所属集合（查询对应的树的根节点），这可以用于判断两个元素是否属于同一集合。

• 并查集用在一些有 N 个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。这个过程看似并不复杂，但数据量极大，若用其他的数据结构来描述的话，往往在空间上过大，计算机无法承受，也无法在短时间内计算出结果，所以只能用并查集来处理。此外，并查集在经过修改后可以支持单个元素的删除、移动；使用动态开点线段树还可以实现可持久化并查集。

注意：并查集无法以较低复杂度实现集合的分离。

并查集的构造：数组

初始化

public UnionFindSet{
    private int[] id;
    private int count;
    public UnionFind1(int n) {
        count = n;
        id = new int[n];// 初始化, 每一个id[i]指向自己, 没有合并的元素
        for (int i = 0; i < n; i++)
            id[i] = i;
    }
}

合并和查找元素

// 查找过程, 查找元素p所对应的集合编号
private int find(int p) {
    assert p >= 0 && p < count;
    return id[p];
}

// 查看元素p和元素q是否所属一个集合，O(1)复杂度
public boolean isConnected(int p, int q) {
    return find(p) == find(q);
}

// 合并元素p和元素q所属的集合，O(n) 复杂度
public void unionElements(int p, int q) {
    
    int pID = find(p);
    int qID = find(q);
    if (pID == qID) return;

    // 合并过程需要遍历一遍所有元素, 将两个元素的所属集合编号合并
    for (int i = 0; i < count; i++)
        if (id[i] == pID) id[i] = qID;
}

效率分析

在以数组构造并查集的情况下，实际过程中，查找的时间复杂度为$O(1)$，而连接效率并不高，为$O(n)$。再次查看关于并查集的定义，可能会发现：或许，我们可以使用另外的一种方法——树，来实现并查集。

并查集的构造：树

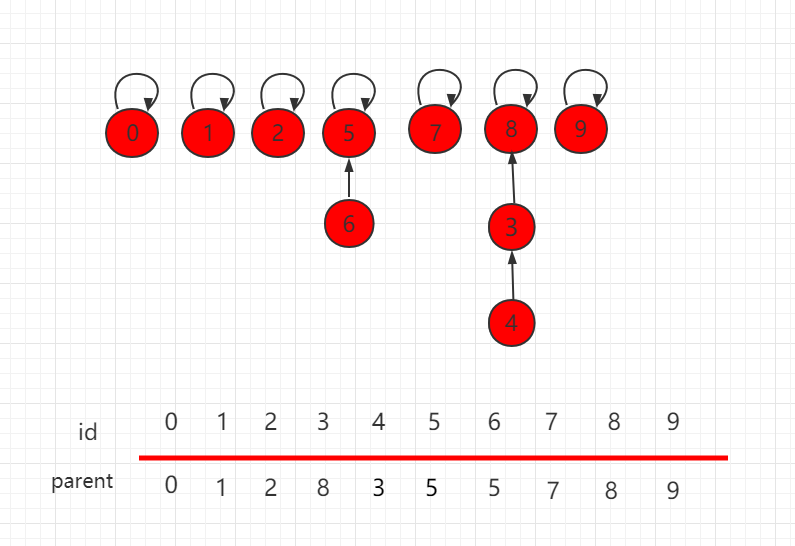
这里，我们使用一个数组构建一棵指向父节点的树。把每一个元素，看做是一个节点并且指向自己的父节点，根节点指向自己。

• 判断两个元素是否连接，只需要判断根节点是否相同即可。
• 连接两个元素，只需要找到它们对应的根节点，使根节点相连，那它们就是相连的节点。

初始化

public class UnionFind2{
    private int[] parent;
    private int count;
    
    public UnionFind2(int count){
        parent = new int[count];
        this.count = count;
         for( int i = 0 ; i < count ; i++)
            parent[i] = i;//初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
    }
}

合并和查找元素

//查找元素p所对应的集合编号, O(h)复杂度
private int find(int p){
    assert( p >= 0 && p < count );
    while( p != parent[p] ) p = parent[p];//根节点的特点: parent[p] == p
    return p;
}

//查看元素p和元素q是否所属一个集合, O(h)复杂度
public boolean isConnected( int p , int q ){
    return find(p) == find(q);
}
//合并元素p和元素q所属的集合, O(h)复杂度
public void unionElements(int p, int q){
    int pRoot = find(p);
    int qRoot = find(q);
    if( pRoot == qRoot ) return;
    parent[pRoot] = qRoot; //合并
}

size的优化

• 对于上述的方法，如果要做unionElements(4,9)的话，就是一步一步地查询4的前驱，遍历完一整棵树后找到了8，然后让9成为8的父亲。
• 这样做的话，开销太大。为此，我们可以采用如下策略：在进行具体指向操作的时候先进行判断，把元素少的集合根节点指向元素多的根节点，能更高概率的生成一个层数比较低的树。
• 为此，我们在构建并查集的时候多引入一个数组参数sz[]，其中，sz[i]表示以i为根节点的元素的个数。

public class UnionFind3{
    private int count;
    private int[] parent;
    private int[] sz;
    
    public UnionFind3(int count){
        this.count=count;
        parent = new int[count];
        sz = ne int[count];
        for( int i = 0 ; i < count ; i ++ ){
            parent[i] = i;
            sz[i] = 1;
        }
    }
    /* Other Methods */
    public void unionElements(int p, int q){

        int pRoot = find(p);
        int qRoot = find(q);

        if( pRoot == qRoot )
            return;

        // 根据两个元素所在树的元素个数不同判断合并方向
        // 将元素个数少的集合合并到元素个数多的集合上
        if( sz[pRoot] < sz[qRoot] ){
            parent[pRoot] = qRoot;
            sz[qRoot] += sz[pRoot];
        }
        else{
            parent[qRoot] = pRoot;
            sz[pRoot] += sz[qRoot];
        }
    }
}

rank的优化

然而，上面的方法还是存在一些问题：如对于下面的例子，如果使用上述方法来操作union(4,2)，则层数反而还会增多。这样，对于较深的元素的合并请求，效率就比较低下。

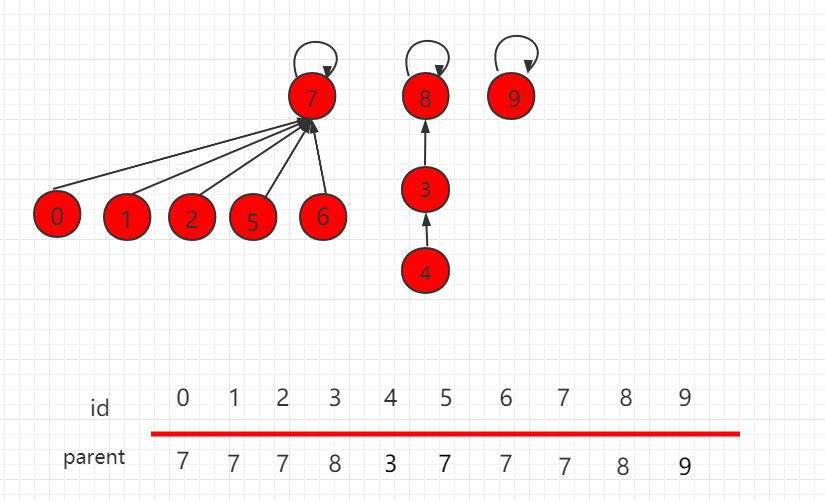
更准确的是，根据两个集合层数，具体判断根节点的指向，层数少的集合根节点指向层数多的集合根节点。这就是rank优化。

为此，我们在构建并查集类时，需要引入的额外参数是rank数组，其中，rank[i]表示以 i 为根的集合所表示的树的层数。

在构造函数中，我们让每一个rank[i]都等于1，parent[i]=i。

合并两元素的时候，需要比较根节点集合的层数，整个过程是 O(h)复杂度，h为树的高度。

public void unionElements(int p, int q){

    int pRoot = find(p);
    int qRoot = find(q);

    if( pRoot == qRoot )
        return;

    if( rank[pRoot] < rank[qRoot] ){
        parent[pRoot] = qRoot;
    }
    else if( rank[qRoot] < rank[pRoot]){
        parent[qRoot] = pRoot;
    }
    else{ // rank[pRoot] == rank[qRoot]
        parent[pRoot] = qRoot;
        rank[qRoot] += 1;   // 维护rank的值
    }
}

find()函数的路径压缩

如果希望能够更加快速的查找到一个根节点，我们就可以对find()函数进行路径压缩。

private int find(int p){
    assert( p >= 0 && p < count );
    // 不断去查询自己的父亲节点, 直到到达根节点
    // 根节点的特点: parent[p] == p
    while( p != parent[p] )
        p = parent[p];
    return p;
}

为了实现更好的压缩效果，可以采用递归的写法。

private int find(int p) {
    assert (p >= 0 && p < count);

    //第二种路径压缩算法
    if (p != parent[p])
        parent[p] = find(parent[p]);
    return parent[p];
}

上述的两种算法的时间复杂度虽然都为$O(h)$，但是树的高度明显降低了，使得其算法和后续的合并算法的耗时更少。

时间复杂度

这里，我们考虑的是使用路径压缩和使用启发式合并的情况。对于上述的两个情况，并查集的每个操作时间为$O(\alpha (n))$，其中，$\alpha$是Ackermann函数的反函数。其增长极其缓慢，也就是说其单次操作的平均运行时间可以认为是一个很小的常数。

Ackermann函数 $A(m,n)$ 的定义为：

$$A(m,n)=\{\begin{array}{ll}n+1,& \text{if }m=0,\\ A(m-1,1),& \text{if }m>0\text{ and }n=0,\\ A(n-1,A(m,n-1)),& \text{otherwise.}\end{array}$$

1. 并查集 - OI Wiki (oi-wiki.org)

2. 并查集从入门到出门 | yukiyama (iyukiyama.github.io)

3. 【算法与数据结构】—— 并查集-CSDN博客