高级搜索树——伸展树

伸展树的简介

伸展树(Splay Tree)是一种二叉搜索树，它通过一系列的旋转操作将被访问的节点调整到树根，从而提高后续访问的速度。伸展树的基本操作包括查找、插入和删除，这些操作的平均时间复杂度为 $O(\log n)$。伸展树是一种自调整的数据结构，它在实际应用中的性能表现优于其他平衡二叉搜索树，如 AVL 树和红黑树。

为什么叫伸展树？

每一次插入一个新元素时，它先像普通的二叉树一样插入到对应的位置，之后，该节点会通过若干次旋转一步一步地向根节点推送并成为新的根节点。由于在左、右旋中，整棵树的形状会发生巨大的改变，且呈现出“伸展”的姿态，故名为“伸展树”。

为什么要提出伸展树？

1. 对于AVL树而言，虽然它的查找、插入和删除操作的时间复杂度都是 $O(\log n)$，但是，其“平衡因子”必须时刻保持在 $\{-1,0,1\}$ 这三个值之间，这就导致了AVL树的旋转操作比较频繁，而且实现起来比较复杂。

2. 局部性：在信息处理的过程中，大量存在着访问的局部性，即刚被访问过的数据很可能在不久之后再次被访问。对于BST来说，在时间上，最近被访问的节点很可能在不久之后再次被访问，而在空间上，下一个将要访问的节点，很可能与刚被访问的节点在空间上相邻。所以，对AVL树而言，连续的$m$次查找，其时间复杂度为$O(m\log n)$。我们可否在局部加速？

   有以下的策略可供借鉴：

   自适应链表：节点一旦被访问，随即移动到最前端；（如果时间足够长，在某一段时间内，所有被访问的元素，都会不约而同地移到列表的前端的位置。）

   模仿：BST的节点一旦被访问，随即调整到树根。（即尽量降低它的深度）

逐层伸展

1. 策略：节点v一旦被访问，则随即被推送至根。（v若是左孩子，就做一次zig()旋转，使得v和其父节点的位置互换；若是右孩子，就做一次zag()旋转。）反复地使用，直到v成为根节点。这里，与其说“推”，不如说“爬”，“一步一步地往上爬”。

2. 实质：就是自下而上的逐层单旋转，使得节点v逐渐向根节点靠拢。

3. 效率分析：伸展过程的效率取决于树的初始形态和节点的访问次序。在最坏情况下，逐层伸展的时间复杂度为$O(n)$，但是，由于节点v在树中的深度是随机的，所以，平均情况下，逐层伸展的时间复杂度为$O(\log n)$。

4. 最坏情况：考虑一棵退化为链表的二叉搜索树。不妨设此时树向左偏，即根节点为最大元素。当访问完该元素时，该节点会被推送至根节点。此时，若从小到大依次访问，则每一个节点所需要的访问成本大致为$n,n-1,\dots ,2,1$。现在，树的形状已经还原成初始形状。访问成本的总和为$\mathrm{\Omega }(n^2)$，分摊下来，逐层伸展的时间复杂度为$\mathrm{\Omega }(n)$。

5. 思考：此时的效率和List/Vector等同，时间复杂度均为$O(n)$；和AVL树的$O(\log n)$相比，也比较差。我们必须寻找一种更好的伸展策略：双层伸展。

双层伸展

1. 自调整二叉搜索树：该算法由D. D. Sleator和R. E. Tarjan于1985年提出。构思的精髓：每一次向上追溯两层，而非一层。反复考察祖孙三代：g=parent(p), p=parent(v),v，并根据三者的相对位置，进行两次适当的旋转操作，使得v上升两层，成为（子）树的根节点。

2. “子孙异侧”：使用zig-zag或zag-zig操作，进行调整：和之前所讲的AVL树的双旋操作完全等效，并且，如此调整的效果，和逐层调整别无二致。

3. “子孙同侧”：使用zig-zig或zag-zag操作，进行调整。注意，这里和之前所讲的AVL树的zig-zig或zag-zag操作的次序不同。

之前所讲的zig-zig和zag-zag都是先父节点开始旋转，而后再是祖父节点，即从下往上的调整、旋转策略；而Tarjan给出的调整策略是，先从祖父节点开始旋转，这样，节点p和v都会上升一层；接下来，再对子树新的树根p（即原来的父节点）进行一次旋转，使得v继续上升一层。

这引发了局部树的拓扑结构的不同。

4. 画龙点睛之笔：Tarjan提出的这个方法，使得节点访问之后，对应的路径长度随即减半，就像含羞草的折叠效果。而且，更重要的是，最坏的情况不会持续发生。此时，伸展操作仅需分摊$O(\log n)$时间。

5. 特例：如果v只有父亲，而没有祖父，则此时必有:v.parent()==T.root()。这种情况下，只需一次旋转即可。

6. “最坏情况”：还是考虑前述的最坏情况，现在访问1，则原树的高度会变低一半：继续访问最低的节点3，会发现，原树的高度继续变低一半。事实上，我们有：伸展树中较深的节点一旦被访问到，对应分支的长度立即减半。更准确地，Tarjan等人采用势能分析法已经证明了，在改用“双层伸展”的策略后，伸展树的单词操作可以在分摊的$O(\log n)$时间内完成。

算法实现

下面是伸展树的具体实现代码。（以下内容来自于OI-wiki）

结构

节点维护的信息：

rt	根节点编号
tot	节点个数
fa[i]	父亲
ch[i][0/1]	左、右儿子编号
val[i]	节点权值
cnt[i]	权值出现的次数
sz[i]	子树大小

操作

maintain(x)：在改变节点位置后，将节点x的size更新。

get(x)：判断节点x是父亲节点的左儿子还是右儿子。

clear(x)：销毁节点x。

void maintain(int x) { sz[x] = sz[ch[x][0]] + sz[ch[x][1]] + cnt[x]; }

bool get(int x) { return x == ch[fa[x]][1]; }

void clear(int x) { ch[x][0] = ch[x][1] = fa[x] = val[x] = sz[x] = cnt[x] = 0; }

旋转

旋转过程：（左、右旋均可）

void rotate(int x) {
  int y = fa[x], z = fa[y], chk = get(x);
  ch[y][chk] = ch[x][chk ^ 1];//y.leftson()->x.rightson(); x.rightson().parent->y;
  if (ch[x][chk ^ 1]) fa[ch[x][chk ^ 1]] = y;
  ch[x][chk ^ 1] = y;
  fa[y] = x;//x.rightson()->y; y.parent()->x;
  fa[x] = z;
  if (z) ch[z][y == ch[z][1]] = x;//if y.parent()==true z.anyson()->x; x.parent()->z;
  maintain(y);
  maintain(x);
}

Splay操作

void splay(int x) {
  for (int f = fa[x]; f = fa[x], f; rotate(x))
    if (fa[f]) rotate(get(x) == get(f) ? f : x);
  rt = x;
}

插入操作

void ins(int k) {
  if (!rt) {
    val[++tot] = k;
    cnt[tot]++;
    rt = tot;
    maintain(rt);
    return;
  }
  int cur = rt, f = 0;
  while (1) {
    if (val[cur] == k) {
      cnt[cur]++;
      maintain(cur);
      maintain(f);
      splay(cur);
      break;
    }
    f = cur;
    cur = ch[cur][val[cur] < k];
    if (!cur) {
      val[++tot] = k;
      cnt[tot]++;
      fa[tot] = f;
      ch[f][val[f] < k] = tot;
      maintain(tot);
      maintain(f);
      splay(tot);
      break;
    }
  }
}

查询x的排名

int rk(int k) {
  int res = 0, cur = rt;
  while (1) {
    if (k < val[cur]) {
      cur = ch[cur][0];
    } else {
      res += sz[ch[cur][0]];
      if (!cur) return res + 1;
      if (k == val[cur]) {
        splay(cur);
        return res + 1;
      }
      res += cnt[cur];
      cur = ch[cur][1];
    }
  }

查询第k名

int kth(int k) {
  int cur = rt;
  while (1) {
    if (ch[cur][0] && k <= sz[ch[cur][0]]) {
      cur = ch[cur][0];
    } else {
      k -= cnt[cur] + sz[ch[cur][0]];
      if (k <= 0) {
        splay(cur);
        return val[cur];
      }
      cur = ch[cur][1];
    }
  }
}

查询前驱、后继

int pre() {
  int cur = ch[rt][0];
  if (!cur) return cur;
  while (ch[cur][1]) cur = ch[cur][1];
  splay(cur);
  return cur;
}
int nxt() {
  int cur = ch[rt][1];
  if (!cur) return cur;
  while (ch[cur][0]) cur = ch[cur][0];
  splay(cur);
  return cur;
}

删除操作

void del(int k) {
  rk(k);
  if (cnt[rt] > 1) {
    cnt[rt]--;
    maintain(rt);
    return;
  }
  if (!ch[rt][0] && !ch[rt][1]) {
    clear(rt);
    rt = 0;
    return;
  }
  if (!ch[rt][0]) {
    int cur = rt;
    rt = ch[rt][1];
    fa[rt] = 0;
    clear(cur);
    return;
  }
  if (!ch[rt][1]) {
    int cur = rt;
    rt = ch[rt][0];
    fa[rt] = 0;
    clear(cur);
    return;
  }
  int cur = rt, x = pre();
  fa[ch[cur][1]] = x;
  ch[x][1] = ch[cur][1];
  clear(cur);
  maintain(rt);
}

最后，将上述内容包含在一个结构体或者类中即可。

参考文献：

1. Sleator, D. D., & Tarjan, R. E. (1985). Self-adjusting binary search trees. Journal of the ACM, 32(3), 652–686. https://doi.org/10.1145/3828.3835

跳表

跳表 (Skip List) 是由 William Pugh 于1989年发明的一种查找数据结构，支持对数据的快速查找，插入和删除。跳跃表以有序的方式在层次化的链表中保存元素， 效率和平衡树媲美 —— 查找、删除、添加等操作都可以在对数期望时间下完成， 并且比起平衡树来说， 跳跃表的实现要简单直观得多。

跳表的期望空间复杂度为 $O(n)$，跳表的查询，插入和删除操作的期望时间复杂度都为 $O(\log n)$。

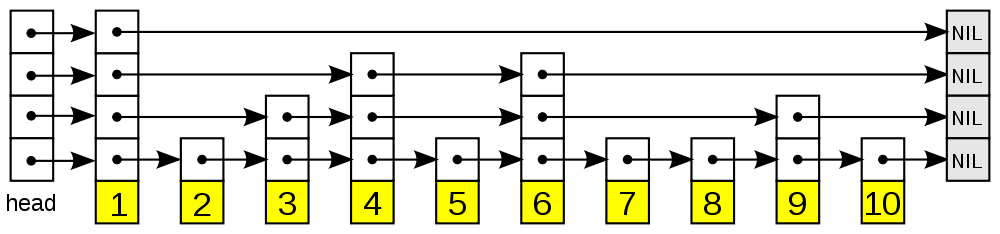
基本思想

跳表是一种类似于链表的数据结构。更加准确地说，跳表是对有序链表的改进。有序所有的有序链表的默认为升序排序。

跳跃表是节点（这里的节点是Quad-Node）的二维集合。

最底层的链表涵盖了所有的数据，而上层的链表通过省略某些节点，达到了建立索引的效果。并且，越上层的链表，其索引性就越强。

Skip List is a two-dimensional collection of nodes arranged horizontally into levels and vertically into towers.

• Each level is a list $S_i$;

• Each tower contains nodes storing the same entry across consecutive lists (consecutive levels).

• 此外，还要引入两个哨兵节点——MIN_INF, MAX_INF.

A Skip List is implemented with quad-nodes that stores:

• Entry;
• Link to the previous and next node, prev,next;
• Link to the node above and below, above,below.

具体实现

查询(Skip Search)

搜索操作skipSearch(Key k)的原理如下：

• Start at the first node of the top list MIN_INF, then repeat the following steps:
• At the current node p, we compare k with key(next(p)):
  • If k=key(next(p)): return value(next(p));
  • if k<key(next(p)): move down to the next list;
  • if k>key(next(p)): move to the right(Scan forward);
  • If we drop down past the bottom list, k not found (return null).

V& find(const K& key) {
  SkipListNode<K, V>* p = head;

  // 找到该层最后一个键值小于 key 的节点，然后走向下一层
  for (int i = level; i >= 0; --i) {
    while (p->forward[i]->key < key) {
      p = p->forward[i];
    }
  }
  // 现在是小于，所以还需要再往后走一步
  p = p->forward[0];

  // 成功找到节点
  if (p->key == key) return p->value;

  // 节点不存在，返回 INVALID
  return tail->value;
}

插入(Insertion)

插入算法使用了一种随机算法。总的来说，插入算法先使用搜索算法，搜索到要插入的位置，然后把内容插入到最底层的链表；然后，使用某些随机算法，决定其向上传播的次数。

实现原理如下：

• Run skipSearch(k) to find its position of insertion. if a node is found with key k, then overwrite its associated value with v.
• Otherwise, when the next move is to drop down past the bottom list,insert(k,v) immediately after node p in $S_i=S_0$.
• Then filp a coin to determine the height of the tower for inserting (k,v):
  • If it is tail, stop here;
  • If it is head, insert the entry at the appropriate node position in $S_{i+1}$;
  • Go back to the First Step.

void insert(const K &key, const V &value) {
  // 用于记录需要修改的节点
  SkipListNode<K, V> *update[MAXL + 1];

  SkipListNode<K, V> *p = head;
  for (int i = level; i >= 0; --i) {
    while (p->forward[i]->key < key) {
      p = p->forward[i];
    }
    // 第 i 层需要修改的节点为 p
    update[i] = p;
  }
  p = p->forward[0];

  // 若已存在则修改
  if (p->key == key) {
    p->value = value;
    return;
  }

  // 获取新节点的最大层数
  int lv = randomLevel();
  if (lv > level) {
    lv = ++level;
    update[lv] = head;
  }

  // 新建节点
  SkipListNode<K, V> *newNode = new SkipListNode<K, V>(key, value, lv);
  // 在第 0~lv 层插入新节点
  for (int i = lv; i >= 0; --i) {
    p = update[i];
    newNode->forward[i] = p->forward[i];
    p->forward[i] = newNode;
  }

  ++length;
}

int randomLevel() {
  int lv = 1;
  // MAXL = 32, S = 0xFFFF, PS = S * P, P = 1 / 4
  while ((rand() & S) < PS) ++lv;
  return min(MAXL, lv);
}

删除(Deletion)

删除算法就是删除键值为key的节点。删除节点的过程就是先执行一遍查询的过程，中途记录要删的节点是在哪一些节点的后面，最后再执行删除。每一层最后一个键值小于 key 的节点，就是需要进行修改的节点。删除时，先删除最底下的节点。

• skipSearch(k): if no entry with key is found, return null.
• Otherwise, remove the value at node where k is found, and remove all values of the nodes exactly above this node, keeping only one list containing guard nodes MIN_INF and MAX_INF.

bool erase(const K &key) {
  // 用于记录需要修改的节点
  SkipListNode<K, V> *update[MAXL + 1];

  SkipListNode<K, V> *p = head;
  for (int i = level; i >= 0; --i) {
    while (p->forward[i]->key < key) {
      p = p->forward[i];
    }
    // 第 i 层需要修改的节点为 p
    update[i] = p;
  }
  p = p->forward[0];

  // 节点不存在
  if (p->key != key) return false;

  // 从最底层开始删除
  for (int i = 0; i <= level; ++i) {
    // 如果这层没有 p 删除就完成了
    if (update[i]->forward[i] != p) {
      break;
    }
    // 断开 p 的连接
    update[i]->forward[i] = p->forward[i];
  }

  // 回收空间
  delete p;

  // 删除节点可能导致最大层数减少
  while (level > 0 && head->forward[level] == tail) --level;

  // 跳表长度
  --length;
  return true;
}

效率分析

时间复杂度

当$p={\displaystyle \frac{1}{2}}$时

Use $C(j)$ to denote the expected # of step took for going up $j$ levels, then:

$$\begin{array}{rl}C(j)& =1+0.5C(j-1)+0.5C(j)\\ C(j)& =2j\end{array}$$

Explain: the expected # of step took for going up j levels should be:

• Make one step, then make either:
  • $C(j-1)$ steps if the first step went up, $p={\displaystyle \frac{1}{2}}$;
  • $C(j)$ steps if the first step went left, $p={\displaystyle \frac{1}{2}}$;
• Where $j$ is the # of the levels for the skip list.

Then estimate the # of level h:

• For the insertion algorithm, the probability that a given entry is at level i is equal to the probability of getting i consecutive heads when flipping a coin: ${\displaystyle \frac{1}{2^i}}$. So, $P_i$ that level i has at least one entry is at most $P_i\le {\displaystyle \frac{n}{2^i}}$.

Explain: Because the probability that any of n different events occurs is at most the sum of probabilities that each occurs.

• For a constant $c>1$， the probability of a skip list with level at least $h=c\log n$ is:

  $$$$$$$$

• And $\underset{n\to inf}{lim}P=1$, h smaller than $c\log n$ i s extremely likely to happen. Hence, the # of levels h is $O(\log n)$.

• For the put operation: time cost includes skipSearch——$O(\log n)$; Finding the correct position to promote the node is $O(1)$. So it still costs $O(\log n)$.

• For the deletion operation: time cost includes skipSearch——$O(\log n)$; Finding the node-to-delete is $O(1)$. So it still costs $O(\log n)$.

更一般的情况

从后向前分析查找路径，这个过程可以分为从最底层爬到第 $L(n)$ 层和后续操作两个部分。在分析时，假设一个节点的具体信息在它被访问之前是未知的。

假设当前我们处于一个第 $i$ 层的节点 $x$，我们并不知道 $x$ 的最大层数和 $x$ 左侧节点的最大层数，只知道 $x$ 的最大层数至少为 $i$。如果 $x$ 的最大层数大于 $i$，那么下一步应该是向上走，这种情况的概率为 $p$；如果 $x$ 的最大层数等于 $i$，那么下一步应该是向左走，这种情况概率为 $1-p$。

令 $C(i)$ 为在一个无限长度的跳表中向上爬 $i$ 层的期望代价，那么有：

$$\begin{array}{rl}C(0)& =0\\ C(i)& =(1-p)(1+C(i))+p(1+C(i-1))\end{array}$$

解得 $C(i)={\displaystyle \frac{i}{p}}$。

由此可以得出：在长度为 $n$ 的跳表中，从最底层爬到第 $L(n)$ 层的期望步数存在上界 ${\displaystyle \frac{L(n)-1}{p}}$。

现在只需要分析爬到第 $L(n)$ 层后还要再走多少步。易得，到了第 $L(n)$ 层后，向左走的步数不会超过第 $L(n)$ 层及更高层的节点数总和，而这个总和的期望为 ${\displaystyle \frac{1}{p}}$。所以到了第 $L(n)$ 层后向左走的期望步数存在上界 ${\displaystyle \frac{1}{p}}$。同理，到了第 $L(n)$ 层后向上走的期望步数存在上界 ${\displaystyle \frac{1}{p}}$。

所以，跳表查询的期望查找步数为 ${\displaystyle \frac{L(n)-1}{p}}+{\displaystyle \frac{2}{p}}$，又因为 $L(n)={\log }_{\frac{1}{p}}n$，所以跳表查询的 期望时间复杂度 为 $O(\log n)$。

在最坏的情况下，每一层有序链表等于初始有序链表，查找过程相当于对最高层的有序链表进行查询，即跳表查询操作的 最差时间复杂度 为 $O(n)$。

插入操作和删除操作就是进行一遍查询的过程，途中记录需要修改的节点，最后完成修改。易得每一层至多只需要修改一个节点，又因为跳表期望层数为 ${\log }_{\frac{1}{p}}n$，所以插入和修改的 期望时间复杂度 也为 $O(\log n)$。

空间复杂度

对于一个节点而言，节点的最高层数为 $i$ 的概率为 $p^{i-1}(1-p)$。所以，跳表的期望层数为 $\sum _{i>=1}i{p}^{i-1}(1-p)={\displaystyle \frac{1}{1-p}}$，且因为 $p$ 为常数，所以跳表的 期望空间复杂度 为 $O(n)$。

在最坏的情况下，每一层有序链表等于初始有序链表，即跳表的 最差空间复杂度 为 $O(n\log n)$。

跳表的随机访问优化

访问跳表中第 $k$ 个节点，相当于访问初始有序链表中的第 $k$ 个节点，很明显这个操作的时间复杂度是 $O(n)$ 的，并不足够优秀。

跳表的随机访问优化就是对每一个前向指针，再多维护这个前向指针的长度。假设 $A$ 和 $B$ 都是跳表中的节点，其中 $A$ 为跳表的第 $a$ 个节点，$B$ 为跳表的第 $b$ 个节点 $(a<b)$，且在跳表的某一层中 $A$ 的前向指针指向 $B$，那么这个前向指针的长度为 $b-a$。

现在访问跳表中的第 $k$ 个节点，就可以从顶层开始，水平地遍历该层的链表，直到当前节点的位置加上当前节点在该层的前向指针长度大于等于 $k$，然后移动至下一层。重复这个过程直至到达第一层且无法继续行操作。此时，当前节点就是跳表中第 $k$ 个节点。

这样，就可以快速地访问到跳表的第 $k$ 个元素。可以证明，这个操作的时间复杂度为 $O(\log n)$。

B-树

B-树的简介

1. 在计算机科学中，B 树（B-tree）是一种自平衡的树，能够保持数据有序。这种数据结构能够让查找数据、顺序访问、插入数据及删除的动作，都在对数时间内完成。
2. B树和B-树是同一种数据结构，只是在不同的文献中，有时候会使用不同的名称。B树是由Rudolf Bayer 和 Edward M. McCreight 提出的。而B+树和B*树和B树是不同的数据结构。
3. 在 B 树中，有两种节点：
   1. 内部节点（internal node）：存储了数据以及指向其子节点的指针。
   2. 叶子节点（leaf node）：与内部节点不同的是，叶子节点只存储数据，并没有子节点。
4. 注意：B树保留了自平衡的特点，但 B 树的每个节点可以拥有两个以上的子节点，因此 B 树是一种多路搜索树。

B-树要解决的问题

1. B树最初是为了解决不同存储级别在访问速度上的巨大差异而设计的，即为了实现高效的IO操作。
2. 有以下几个事实，使得B树作为一种等效的二叉搜索树依然被广泛使用：

   1. 存储器容量的增长速度 << 应用问题规模的增长速度。随着数据量惊人的增加，尽管内存的规格也在不断增加，然而每单位的内存所要处理的数据量也在不断地增加。相对而言，存储器的容量实际上在不断减小！

   2. 在特定工艺及成本下，存储器都是容量与速度的折中产物。注意到，存储器越大、越快，成本也越高；而存储器容量越大/小，访问速度越慢/快！

   3. 实用的存储系统，由不同类型的存储器级联而成，以综合其各自的优势。不同类型的存储器，容量、访问速度差异悬殊。二者差异的数量级在${10}^5$。若一次内存访问需要一秒，则一次磁盘访问就需一天；为避免一次磁盘访问，我们宁愿访问内存1000次。所以，多数的存储系统，都是分级组织的。

   4. 在外存读写1B，与读写1KB几乎一样快。这是因为外存的读写是以块/页为单位的，而不是以字节为单位的。（批量式）。比如，在C语言的<stdio.h>中，我们有

      #define BUFSIZ 512 //缓冲区默认容量
      int setvbuf( //定制缓冲区
      	FILE* fp, //流
      	char* buf, //缓冲区
      	int _Mode, //_IOFBF | _IOLBF | _IONBF
      	size_t size); //缓冲区容量
      int fflush( FILE* fp );

      这样一段代码，它可以实现定制缓冲区的功能。这样，以页（page）为单位，借助缓冲区批量访问，可大大缩短单位字节的平均访问时间。

3. 分级存储——利用数据访问的局部性
   1. 机制与策略：常用的数据，复制到更高层、更小的存储器中；若找不到，才向更低层、更大的存储器索取。
   2. 算法的实际运行时间，主要取决于相邻存储级别之间数据传输（I/O）的速度与次数。

B-树的构成和性质

1. 一棵 $m$ 阶的 B 树满足的性质如下，其中$m$ 表示这个树的每一个节点最多可以拥有的子节点个数：（ $m$ 阶的 B 树，即$m$路平衡搜索树，$m\ge 2$）

   1. 每个节点最多有 $m$ 个子节点。

   2. 每一个非叶子节点（除根节点）最少有 $\lceil {\displaystyle \frac{m}{2}}\rceil$ 个子节点。（此时可以称作$(\lceil {\displaystyle \frac{m}{2}}\rceil ,m)$树）

      4阶B-树，即(2, 4)树，和红黑树有很深的联系。

   3. 如果根节点不是叶子节点，那么它至少有两个子节点。（“修正案”）

   4. 有 $k$ 个子节点的非叶子节点拥有 $k-1$ 个键，且升序排列，满足 $k[i]<k[i+1]$。

   5. 每个节点至多包含 $2k-1$ 个键。

   6. 所有的叶子节点都在同一层。（理想平衡）

   B-树的外部节点（external node）更加名副其实：它们实际上未必意味着查找失败， 而可能表示目标关键码存在于更低层次的某一外部存储系统中，顺着该节点的指示，即可深入至 下一级存储系统并继续查找。正因为如此，不同于常规的搜索树，在计算B-树 高度时，还需要计入其最底层的外部节点。

   来自：数据结构（C++语言版）（第三版），邓俊辉，清华大学出版社，ISBN：978-7-302-33064-6，214页。DSACPP (tsinghua.edu.cn)

   B-树的图例如下：（相较于BST，B-树会显得更宽、更矮。在此时的画法中，存有指针并指向其子节点的的节点以圆圈表示，而所有的外部节点均不再画出。）

   

2. B-树被定义为一种平衡的多路搜索树。并且经过适当的合并，能够得到一些超级节点。具体对于一棵普通的BST来说，若每两代节点合并，则会形成一个超级节点，在节点中，父亲和左、右两个孩子并列，一共有3个关键码。同时，该超级节点也拥有四个分支，为原先第三代的分支。所以，若每m代节点合并，则会形成一个超级节点，其中有$2^m-1$个关键码，同时拥有$2^m$个分支。这在逻辑上和BBST完全等价。

3. 多级存储系统中如果使用B树，可以针对外部查找而大大减少I/O的次数。如果有$1G={10}^9$个数据，则形成的AVL树大概有${\log }_2({10}^9)\approx 30$层，每一次需要一次I/O操作。用这么多的操作，每一次仅仅读出一个关键码，得不偿失；而B-依靠着超级节点这一特性，使得每一次下降一层，都以超级节点为单位，读出一组关键码。具体来说，一般一组的大小取决于磁盘等外存本身所设定的数据缓冲页面的大小。

B-树的优点

之前已经介绍过二叉查找树。但是这类型数据结构的问题在于，由于每个节点只能容纳一个数据，导致树的高度很高，逻辑上挨着的节点数据可能离得很远。

考虑在磁盘中存储数据的情况，与内存相比，读写磁盘有以下不同点：

1. 读写磁盘的速度相比内存读写慢很多。
2. 每次读写磁盘的单位要比读写内存的最小单位大很多。

由于读写磁盘的这个特点，因此对应的数据结构应该尽量的满足「局部性原理」：「当一个数据被用到时，其附近的数据也通常会马上被使用」，为了满足局部性原理， 所以应该将逻辑上相邻的数据在物理上也尽量存储在一起。这样才能减少读写磁盘的数量。

所以，对比起一个节点只能存储一个数据的 BST 类数据结构来，要求这种数据结构在形状上更「胖」、更加「扁平」，即：每个节点能容纳更多的数据， 这样就能降低树的高度，同时让逻辑上相邻的数据都能尽量存储在物理上也相邻的硬盘空间上，减少磁盘读写。

B-树的实现

与 二叉搜索树 类似，B 树的基本操作有查找，遍历，插入，删除。（以下内容来自B 树 - OI Wiki (oi-wiki.org)）

查找

B 树中的节点包含有多个键。假设需要查找的是 $k$，那么从根节点开始，从上到下递归的遍历树。在每一层上，搜索的范围被减小到包含了搜索值的子树中。 子树值的范围被它的父节点的键确定。因为是从根节点开始的二分法查找，所以查找一个键的代码如下：

BTreeNode *BTreeNode::search(int k) {
  // 找到第一个大于等于待查找键 k 的键
  int i = 0;
  while (i < n && k > keys[i]) i++;

  // 如果找到的第一个键等于 k , 返回节点指针
  if (keys[i] == k) return this;

  // 如果没有找到键 k 且当前节点为叶子节点则返回NULL
  if (leaf == true) return NULL;

  // 递归
  return C[i]->search(k);
}

遍历

和二叉树的中序遍历十分相似。

void BTreeNode::traverse() {
  // 有 n 个键和 n+1 个孩子
  // 遍历 n 个键和前 n 个孩子
  int i;
  for (i = 0; i < n; i++) {
    // 如果当前节点不是叶子节点, 在打印 key[i] 之前,
    // 先遍历以 C[i] 为根的子树.
    if (leaf == false) C[i]->traverse();
    cout << " " << keys[i];
  }

  // 打印以最后一个孩子为根的子树
  if (leaf == false) C[i]->traverse();
}

插入

为了方便表述，插入设定为在以 $o$ 为根节点的 B 树中插入一个值为 $v$ 的新节点。

一个新插入的 $v$ 总是被插入到叶子节点。与二叉搜索树的插入操作类似，从根节点开始，向下遍历直到叶子节点，将值为 $v$ 的新节点插入到相应的叶子节点。 与二叉搜索树不同的是，通过最小度定义了一个节点可以包含键的个数的一个取值范围，所以在插入一个新节点时，就需要确认插入这个叶子节点之后，它的父节点是否超出该节点本身最大可容纳的节点个数。（检查是否该叶子节点的关键字数是否小于$m-1$）

针对一棵高度为 $h$ 的 $m$ 阶 B 树，插入一个元素时，首先要验证该元素在 B 树中是否存在，如果不存在，那么就要在叶子节点中插入该新的元素，此时分 3 种情况：

1. 如果叶子节点空间足够，即该节点的关键字数小于 $m-1$，则直接插入在叶子节点的左边或右边；

2. 如果空间满了以至于没有足够的空间去添加新的元素，即该节点的关键字数已经有了 $m$ 个，则需要将该节点进行「分裂」，将一半数量的关键字元素分裂到新的其相邻右节点中，中间关键字元素上移到父节点中，而且当节点中关键元素向右移动了，相关的指针也需要向右移。

   1. 从该节点的原有元素和新的元素中选择出中位数
   2. 小于这一中位数的元素放入左边节点，大于这一中位数的元素放入右边节点，中位数作为分隔值。
   3. 分隔值被插入到父节点中，这可能会造成父节点分裂，分裂父节点时可能又会使它的父节点分裂，以此类推。如果没有父节点（这一节点是根节点），就创建一个新的根节点（增加了树的高度）。

3. 如果一直分裂到根节点，那么就需要创建一个新的根节点。它有一个分隔值和两个子节点。（即整棵树向上“拔高”一层）

这就是根节点并不像内部节点一样有最少子节点数量限制的原因。每个节点中元素的最大数量是 $U-1$。当一个节点分裂时，一个元素被移动到它的父节点，但是一个新的元素增加了进来。所以最大的元素数量 $U-1$ 必须能够被分成两个合法的节点。 如果 $U-1$ 是奇数，那么 $U=2L$，总共有 $2L-1$ 个元素，一个新的节点有 $L-1$ 个元素，另外一个有 $L$ 个元素，都是合法的节点。如果 $U-1$ 是偶数，那么 $U=2L-1$, 总共有 $2L-2$ 个元素。一半是 $L-1$，正好是节点允许的最小元素数量。

这里，从e2到e3，元素84被上移一层。对于超级节点77-84-89来说，84是77，89的父亲，所以，在上移后，原53->84的指向放置于新生成的超级节点中，而多出来的两个点位，则用来让84指向它的两个孩子——77,89。从e3到e4，由于在根节点即将发生上溢，所以需要将原根超级节点拆除，代之以一个新的上移一层的根节点和两棵子树。

代码：

void BTree::insert(int k) {
  // 如果树为空树
  if (root == NULL) {
    // 为根节点分配空间
    root = new BTreeNode(t, true);
    root->keys[0] = k;  // 插入节点 k
    root->n = 1;        // 更新根节点的关键字的个数为 1
  } else {
    // 当根节点已满，则对B-树进行生长操作
    if (root->n == 2 * t - 1) {
      // 为新的根节点分配空间
      BTreeNode *s = new BTreeNode(t, false);

      // 将旧的根节点作为新的根节点的孩子
      s->C[0] = root;

      // 将旧的根节点分裂为两个，并将一个关键字上移到新的根节点
      s->splitChild(0, root);

      // 新的根节点有两个孩子节点
      // 确定哪一个孩子将拥有新插入的关键字
      int i = 0;
      if (s->keys[0] < k) i++;
      s->C[i]->insertNonFull(k);

      // 新的根节点更新为 s
      root = s;
    } else  // 根节点未满，调用 insertNonFull() 函数进行插入
      root->insertNonFull(k);
  }
}

// 将关键字 k 插入到一个未满的节点中
void BTreeNode::insertNonFull(int k) {
  // 初始化 i 为节点中的最后一个关键字的位置
  int i = n - 1;

  // 如果当前节点是叶子节点
  if (leaf == true) {
    // 下面的循环做两件事：
    // a) 找到新插入的关键字位置并插入
    // b) 移动所有大于关键字 k 的向后移动一个位置
    while (i >= 0 && keys[i] > k) {
      keys[i + 1] = keys[i];
      i--;
    }

    // 插入新的关键字，节点包含的关键字个数加 1
    keys[i + 1] = k;
    n = n + 1;
  } else {
    // 找到第一个大于关键字 k 的关键字 keys[i] 的孩子节点
    while (i >= 0 && keys[i] > k) i--;

    // 检查孩子节点是否已满
    if (C[i + 1]->n == 2 * t - 1) {
      // 如果已满，则进行分裂操作
      splitChild(i + 1, C[i + 1]);

      // 分裂后，C[i] 中间的关键字上移到父节点，
      // C[i] 分裂称为两个孩子节点
      // 找到新插入关键字应该插入的节点位置
      if (keys[i + 1] < k) i++;
    }
    C[i + 1]->insertNonFull(k);
  }
}

// 节点 y 已满，则分裂节点 y
void BTreeNode::splitChild(int i, BTreeNode *y) {
  // 创建一个新的节点存储 t - 1 个关键字
  BTreeNode *z = new BTreeNode(y->t, y->leaf);
  z->n = t - 1;

  // 将节点 y 的后 t -1 个关键字拷贝到 z 中
  for (int j = 0; j < t - 1; j++) z->keys[j] = y->keys[j + t];

  // 如果 y 不是叶子节点，拷贝 y 的后 t 个孩子节点到 z中
  if (y->leaf == false) {
    for (int j = 0; j < t; j++) z->C[j] = y->C[j + t];
  }

  // 将 y 所包含的关键字的个数设置为 t -1
  // 因为已满则为2t -1 ，节点 z 中包含 t - 1 个
  // 一个关键字需要上移
  // 所以 y 中包含的关键字变为 2t-1 - (t-1) -1
  y->n = t - 1;

  // 给当前节点的指针分配新的空间，
  // 因为有新的关键字加入，父节点将多一个孩子。
  for (int j = n; j >= i + 1; j--) C[j + 1] = C[j];

  // 当前节点的下一个孩子设置为z
  C[i + 1] = z;

  // 将所有父节点中比上移的关键字大的关键字后移
  // 找到上移节点的关键字的位置
  for (int j = n - 1; j >= i; j--) keys[j + 1] = keys[j];

  // 拷贝 y 的中间关键字到其父节点中
  keys[i] = y->keys[t - 1];

  // 当前节点包含的关键字个数加 1
  n = n + 1;
}

删除

树的删除操作相比于插入操作更为复杂，因为删除之后经常需要重新排列节点。

与 B 树的插入操作类似，必须确保删除操作不违背 B 树的特性。正如插入操作中每一个节点所包含的键的个数不能超过 $2k-1$ 一样，删除操作要保证每一个节点包含的键的个数不少于 $k-1$ 个（除根节点允许包含比 $k-1$ 少的关键字的个数）。

有两种常用的删除策略：

1. 定位并删除元素，然后调整树使它满足约束条件。
2. 从上到下处理这棵树，在进入一个节点之前，调整树使得之后一旦遇到了要删除的键，它可以被直接删除而不需要再进行调整。

下面介绍使用第一种策略的删除。

首先，查找 B 树中需删除的元素，如果该元素在 B 树中存在，则将该元素在其节点中进行删除；删除该元素后，首先判断该元素是否有左右孩子节点， 如果有，则上移孩子节点中的某相近元素（「左孩子最右边的节点」或「右孩子最左边的节点」）到父节点中，然后是移动之后的情况；如果没有，直接删除。

1. 某节点中元素数目小于 $m/2-1$，$m/2$ 向上取整，则需要看其某相邻兄弟节点是否丰满。
2. 如果丰满（节点中元素个数大于 $m/2-1$），则向父节点借一个元素来满足条件。
3. 如果其相邻兄弟都不丰满，即其节点数目等于 $m/2-1$，则该节点与其相邻的某一兄弟节点进行「合并」成一个节点。

接下来用一个 5 阶 B 树为例，详细讲解删除的操作。

如图所示，接下来要依次删除 8，20，18，5。 首先要删除元素 8。先查找到元素 8 在叶子节点中，删除 8 后叶子节点的元素个数为 2，符合 B 树的规则。然后需要把元素 11 和 12 都向前移动一位。完成后如图所示。

下一步，删除 20，因为 20 没有在叶子节点中，而是在中间节点中找到，可以发现 20 的继承者是 23（字母升序的下个元素），然后需要将 23 上移到 20 的位置，之后将孩子节点中的 23 进行删除。 删除后检查一下，该孩子节点中元素个数大于 2，无需进行合并操作。

所以这一步之后，B 树如下图所示。

下一步删除 18，18 在叶子节点中，但是该节点中元素数目为 2，删除导致只有 1 个元素，已经小于最小元素数目 2。 而由前面已经知道：如果其某个相邻兄弟节点中比较丰满（元素个数大于 $\lceil {\displaystyle \frac{5}{2}}\rceil$），则可以向父节点借一个元素，然后将最丰满的相邻兄弟节点中上移最后或最前一个元素到父节点中。 在这个实例中，右相邻兄弟节点中比较丰满（3 个元素大于 2），所以先向父节点借一个元素 23 下移到该叶子节点中，代替原来 19 的位置。19 前移。 然后 24 在相邻右兄弟节点中，需要上移到父节点中。最后在相邻右兄弟节点中删除 24，后面的元素前移。

这一步之后，B 树如下图所示。

最后一步需要删除元素 5，但是删除后会导致很多问题。因为 5 所在的节点数目刚好达标也就是刚好满足最小元素个数 2。 而相邻的兄弟节点也是同样的情况，删除一个元素都不能满足条件，所以需要该节点与某相邻兄弟节点进行合并操作；首先移动父节点中的元素（该元素在两个需要合并的两个节点元素之间）下移到其子节点中。 然后将这两个节点进行合并成一个节点。所以在该实例中，首先将父节点中的元素 4 下移到已经删除 5 而只有 6 的节点中，然后将含有 4 和 6 的节点和含有 1，3 的相邻兄弟节点进行合并成一个节点。

这一步之后，B 树如下图所示。

但是这里观察到父节点只包含了一个元素 7，这就没有达标（因为非根节点包括叶子节点的元素数量 必须满足于 ，而此处的 ）。 如果这个问题节点的相邻兄弟比较丰满，则可以向父节点借一个元素。而此时兄弟节点元素刚好为 2，刚刚满足，只能进行合并，而根节点中的唯一元素 13 下移到子节点。 这样，树的高度减少一层。

所以最终的效果如下图。

伪代码如下：

B-Tree-Delete-Key(x, k) 
if not leaf[x] then 
    y ← Preceding-Child(x) 
    z ← Successor-Child(x) 
    if n[[y] > t − 1 then 
        k' ← Find-Predecessor-Key(k, x)]() 
        Move-Key(k', y, x) 
        Move-Key(k, x, z) 
        B-Tree-Delete-Key(k, z) 
    else if n[z] > t − 1 then 
        k' ← Find-Successor-Key(k, x) 
        Move-Key(k', z, x) 
        Move-Key(k, x, y) 
        B-Tree-Delete-Key(k, y) 
    else 
        Move-Key(k, x, y) 
        Merge-Nodes(y, z) 
        B-Tree-Delete-Key(k, y) 
    else (leaf node) 
    y ← Preceding-Child(x) 
    z ← Successor-Child(x) 
    w ← root(x) 
    v ← RootKey(x) 
        if n[x] > t − 1 then Remove-Key(k, x) 
        else if n[y] > t − 1 then 
            k' ← Find-Predecessor-Key(w, v) 
            Move-Key(k', y,w) 
            k' ← Find-Successor-Key(w, v) 
            Move-Key(k',w, x) 
            B-Tree-Delete-Key(k, x) 
        else if n[w] > t − 1 then 
            k' ← Find-Successor-Key(w, v) 
            Move-Key(k', z,w) 
            k' ← Find-Predecessor-Key(w, v) 
            Move-Key(k',w, x) 
            B-Tree-Delete-Key(k, x) 
        else 
            s ← Find-Sibling(w) 
            w' ← root(w) 
                if n[w'] = t − 1 then 
                    Merge-Nodes(w',w) 
                    Merge-Nodes(w, s) 
                    B-Tree-Delete-Key(k, x)
                else
                    Move-Key(v,w, x)
                    B-Tree-Delete-Key(k, x)