图的概述

图的定义

图 (graph) 是一个二元组 $G = (V (G), E (G))$ 。其中 $V (G)$ 是非空集，称为 点集 (vertex set)，对于 $V$ 中的每个元素，我们称其为 顶点 (vertex) 或 节点 (node)，简称点； $E (G)$ 为 $V (G)$ 各结点之间边的集合，称为 边集 (edge set)，对于 $E$ 中的每个元素（即某一对顶点(u, v)），我们称其为 边(edge) 或 弧 (arc)。常用 $G = (V, E)$ 表示图。
阶 (order)：图 $G$ 的阶是指 $V (G)$ 的元素个数，记作 $| V (G) |$ 或 $n$ 。
有限图和无限图：当 $V, E$ 都是有限集合时，称 $G$ 为有限图；当 $V$ 或 $E$ 是无限集合时，称 $G$ 为无限图。
有向图、无向图、混合图：根据边是否有方向，图可分为有向图和无向图。有向图中的边是有方向的，无向图中的边是无方向的。混合图中既有有向边，又有无向边。
- 若 $G$ 为无向图，则 $E$ 中的每个元素为一个无序二元组 $(u, v)$ ，称作 无向边 (undirected edge)，简称 边 (edge)，其中 $u, v \in V$ 。设 $e = (u, v)$ ，则 $u$ 和 $v$ 称为 $e$ 的 端点 (endpoint)。
- 若 $G$ 为有向图，则 $E$ 中的每一个元素为一个有序二元组 $(u, v)$ ，有时也写作 $u \to v$ ，称作 有向边 (directed edge) 或 弧 (arc)，在不引起混淆的情况下也可以称作 边 (edge)。设 $e = u \to v$ ，则此时 $u$ 称为 $e$ 的 起点 (tail)， $v$ 称为 $e$ 的 终点 (head)，起点和终点也称为 $e$ 的 端点 (endpoint)。并称 $u$ 是 $v$ 的直接前驱， $v$ 是 $u$ 的直接后继。
为什么起点是 tail，终点是 head？ 边通常用箭头表示，而箭头是从「尾」指向「头」的。
- 若 $G$ 为混合图，则 $E$ 中既有 有向边，又有 无向边。
这里，以有向图的实现为重点，因为一条无向边可以由一对有向边 $(u, v)$ 和 $(v, u)$ 来间接表示。
权：若 $G$ 的每条边 $e_{k} = (u_{k}, v_{k})$ 都被赋予一个数作为该边的权，则称 $G$ 为 赋权图。如果这些权都是正实数，就称 $G$ 为 正权图。

相邻

在无向图 $G = (V, E)$ 中，若点 $v$ 是边 $e$ 的一个端点，则称 $v$ 和 $e$ 是 关联的 (incident) 。对于两顶点 $u$ 和 $v$ ，若存在边 $(u, v)$ ，则称 $u$ 和 $v$ 是 邻接的 (adjacent)。

邻接关系：指两顶点之间的关系；
关联关系：指一个顶点和连接其的一条边之间的关系。

一个顶点 $v \in V$ 的 邻域 (neighborhood) 是所有与之相邻的顶点所构成的集合，记作 $N (v)$ 。

一个点集 $S$ 的邻域是所有与 $S$ 中至少一个点相邻的点所构成的集合，记作 $N (S)$ ，即：

N (S) = ⋃_{v \in S} N (v)

简单图

自环 (loop)：对 $E$ 中的边 $e = (u, v)$ ，若 $u = v$ ，则 $e$ 被称作一个自环。

重边 (multiple edge)：若 $E$ 中存在两个完全相同的元素（边） $e_{1}, e_{2}$ ，则它们被称作（一组）重边。

简单图 (simple graph)：若一个图中没有自环和重边，它被称为简单图。具有至少两个顶点的简单无向图中一定存在度相同的结点。（鸽巢原理）

如果一张图中有自环或重边，则称它为 多重图 (multigraph)。

在无向图中 $(u, v)$ 和 $(v, u)$ 算一组重边，而在有向图中， $u \to v$ 和 $v \to u$ 不为重边。在题目中，如果没有特殊说明，是可以存在自环和重边的，在做题时需特殊考虑。

路径和环路

途径(Walk)：是由 $m + 1$ 个顶点和 $m$ 条边交替而成的一个序列，其中每条边的终点是下一条边的起点。记作

π = {v_{0}, e_{1}, v_{1}, e_{2}, v_{2}, \dots, e_{m}, v_{m}}, \forall i \in (0, m], e_{i} = (v_{i - 1}, v_{i}) .

为了简化描述，也可以只标出顶点序列，即 $π = {v_{0}, v_{1}, \dots, v_{m}}$ 。一般地，通路的长度为边的数量 $m$ ，记作 $| π | = m$ 。如果边是带权的，长度通常指途径上的边权之和。

迹 (Trail)：对于一条途径 $w$ ，若 $e_{1}, e_{2}, \dots, e_{k}$ 两两互不相同，则称 $w$ 是一条迹。迹不走回头路。

路径(Path)：对于一条迹 $t$ ，若其连接的点的序列中点两两不同，则称 $t$ 是一条路径。也就是说，路径既不走回头路，也不重复走过某一点。

项目	Vertex1?=Vertex2	Edge1?=Edge2
Walk	可以相等	可以相等
Trail	可以相等	不等
Path	不等	不等

回路 (Circuit)：对于一条迹 $t$ ，若 $v_{0} = v_{k}$ ，则称 $t$ 是一条回路。

环/圈 (Cycle)（又称 简单回路/简单环 (Simple Circuit)）：对于一条回路 $c$ ，若 $v_{0} = v_{k}$ 是点序列中唯一重复出现的点对，则称 $c$ 是一个环。（推荐在表示最后的一个点的时候使用return symbol，代表指向起点，可以更加清晰地表示出环的相关概念）

关于路径的定义在不同地方可能有所不同，如，「路径」可能指本文中的「途径」，「环」可能指本文中的「回路」。如果在题目中看到类似的词汇，且没有「简单路径」/「非简单路径」（即本文中的「途径」）等特殊说明，最好询问一下具体指什么。

有向无环图：不含任何环路的有向图，称为有向无环图（Directed Acylic Graph, DAG）。

欧拉环路(Eulerian Tour)：经过图中每条边一次且仅一次的环路。其长度为图中边的数量。实例：一笔画问题。
哈密顿环路(Hamiltonian Cycle)：经过图中每个顶点一次且仅一次的环路。

度数

与一个顶点 $v$ 关联的边的条数称作该顶点的 度 (Degree)，记作 $d (v)$ 。特别地，对于边 $(v, v)$ ，则每条这样的边要对 $d (v)$ 产生 $2$ 的贡献。特别地，对于无向简单图，有 $d (v) = | N (v) |$ 。
握手定理（又称图论基本定理）：对于任何无向图 $G = (V, E)$ ，有 $\sum_{v \in V} d (v) = 2 | E |$ 。
- 推论1：在任意图中，度数为奇数的点必然有偶数个。
- 推论2：The number of edges is $O (n^{2})$ in a complete graph that has n vertices.

若 $d (v) = 0$ ，则称 $v$ 为 孤立点 (Isolated Vertex)。
若 $d (v) = 1$ ，则称 $v$ 为 叶节点 (Leaf Vertex)/悬挂点 (Pendant Vertex)。
若 $2 ∣ d (v)$ ，则称 $v$ 为 偶点 (Even Vertex)。
若 $2 ∤ d (v)$ ，则称 $v$ 为 奇点 (Odd Vertex)。图中奇点的个数是偶数。
若 $d (v) = | V | - 1$ ，则称 $v$ 为 支配点 (Universal Vertex)。

对一张图，所有节点的度数的最小值称为 $G$ 的 最小度 (Minimum Degree)，记作 $δ (G)$ ；最大值称为 最大度 (Maximum Degree)，记作 $Δ (G)$ 。即： $δ (G) = min_{v \in G} d (v)$ ， $Δ (G) = max_{v \in G} d (v)$ 。
在有向图 $G = (V, E)$ 中，以一个顶点 $v$ 为起点的边的条数称为该顶点的 出度 (out-degree)，记作 $d^{+} (v)$ 或 $outdeg (v)$ 。以一个顶点 $v$ 为终点的边的条数称为该节点的 入度 (in-degree)，记作 $d^{-} (v)$ 或 $indeg (v)$ 。显然 $d^{+} (v) + d^{-} (v) = d (v)$ 。
对于任何有向图 $G = (V, E)$ ，有：

\sum_{v \in V} d^{+} (v) = \sum_{v \in V} d^{-} (v) = | E |

若对一张无向图 $G = (V, E)$ ，每个顶点的度数都是一个固定的常数 $k$ ，则称 $G$ 为 $k$ - 正则图 ( $k$ -Regular Graph)。
如果给定一个序列 a，可以找到一个图 G，以其为度数列，则称 a 是 可图化 的。
如果给定一个序列 a，可以找到一个简单图 G，以其为度数列，则称 a 是 可简单图化 的。

子图

子图 (Subgraph)：对一张图 $G = (V, E)$ ，若存在另一张图 $H = (V^{'}, E^{'})$ 满足 $V^{'} \subseteq V$ 且 $E^{'} \subseteq E$ ，则称 $H$ 是 $G$ 的子图，记作 $H \subseteq G$ 。
导出子图(Induced subgraph)：若对 $H \subseteq G$ ，满足 $\forall u, v \in V^{'}$ ，若 $(u, v) \in E$ ，有 $(u, v) \in E^{'}$ ，则称 $H$ 是 $G$ 的导出子图或诱导子图。

一个图的导出子图仅由子图的点集决定，因此点集为 $V^{'}$ ( $V^{'} \subseteq V$ ) 的导出子图称为 $V^{'}$ 导出的子图，记作 $G [V^{'}]$ 。

生成子图(Spanning Subgraph)：若 $H \subseteq G$ 满足 $V^{'} = V$ ，则称 $H$ 为 $G$ 的生成子图或支撑子图。

类型	表示	顶点关系	边关系
无项母图	$G = (V, E)$	$V = V$	$E = E$
子图	$G^{'} = (V^{'}, E^{'})$	$V^{'} \subseteq V$	$E^{'} \subseteq E$
生成子图	$G_{s} = (V_{s}, E_{s})$	$V_{s} = V$	$E_{s} \subseteq E$
节点导出子图	$G (V_{i}) = (V_{i}, E_{i})$	$V_{i} \subseteq V$	$\forall u, v \in V^{'}, (u, v) \in E \to (u, v) \in E^{'}$
边导出子图	$G (E_{i}) = (V_{i}, E_{i})$	$\forall e = (u, v) \in E_{i}, u, v \in V \to u, v \in V_{i}$	$E_{i} \subseteq E$

显然， $G$ 是自身的子图，支撑子图，导出子图；无边图是 $G$ 的支撑子图。原图 $G$ 和无边图都是 $G$ 的平凡子图。
如果一张无向图 $G$ 的某个生成子图 $F$ 为 $k$ - 正则图，则称 $F$ 为 $G$ 的一个 $k$ - 因子 ( $k$ -factor)。
如果有向图 $G = (V, E)$ 的导出子图 $H = G [V^{*}]$ 满足 $\forall v \in V^{*}, (v, u) \in E$ ，有 $u \in V^{*}$ ，则称 $H$ 为 $G$ 的一个 闭合子图 (closed subgraph)。

连通

无向图

对于一张无向图 $G = (V, E)$ ，对于 $u, v \in V$ ，若存在一条途径使得 $v_{0} = u, v_{k} = v$ ，则称 $u$ 和 $v$ 是 连通的 (connected)。由定义，任意一个顶点和自身连通，任意一条边的两个端点连通。

若无向图 $G = (V, E)$ ，满足其中任意两个顶点均连通，则称 $G$ 是 连通图 (connected graph)， $G$ 的这一性质称作 连通性 (connectivity)。

若 $H$ 是 $G$ 的一个连通子图，且不存在 $F$ 满足 $H ⊊ F \subseteq G$ 且 $F$ 为连通图，则 $H$ 是 $G$ 的一个 连通块/连通分量 (connected component)（极大连通子图）。

有向图

对于一张有向图 $G = (V, E)$ ，对于 $u, v \in V$ ，若存在一条途径使得 $v_{0} = u, v_{k} = v$ ，则称 $u$ 可达 $v$ 。由定义，任意一个顶点可达自身，任意一条边的起点可达终点。（无向图中的连通也可以视作双向可达。）

若一张有向图的节点两两互相可达，则称这张图是 强连通的 (strongly connected)。

若一张有向图的边替换为无向边后可以得到一张连通图，则称原来这张有向图是 弱连通的 (weakly connected)。

与连通分量类似，也有 弱连通分量 (weakly connected component)（极大弱连通子图）和 强连通分量 (strongly connected component)（极大强连通子图）。

割

相关算法：割点算法；双连通分量。

在本部分中，有向图的「连通」一般指「强连通」。

对于连通图 $G = (V, E)$ ，若 $V^{'} \subseteq V$ 且 $G [V ∖ V^{'}]$ （即从 $G$ 中删去 $V^{'}$ 中的点）不是连通图，则 $V^{'}$ 是图 $G$ 的一个 点割集 (vertex cut/separating set)。大小为一的点割集又被称作 割点 (cut vertex)。

对于连通图 $G = (V, E)$ 和整数 $k$ ，若 $| V | \geq k + 1$ 且 $G$ 不存在大小为 $k - 1$ 的点割集，则称图 $G$ 是 $k$ - 点连通的 ( $k$ -vertex-connected)，而使得上式成立的最大的 $k$ 被称作图 $G$ 的 点连通度 (vertex connectivity)，记作 $κ (G)$ 。（对于非完全图，点连通度即为最小点割集的大小，而完全图 $K_{n}$ 的点连通度为 $n - 1$ 。）

对于图 $G = (V, E)$ 以及 $u, v \in V$ 满足 $u \neq v$ ， $u$ 和 $v$ 不相邻， $u$ 可达 $v$ ，若 $V^{'} \subseteq V$ ， $u, v \notin V^{'}$ ，且在 $G [V ∖ V^{'}]$ 中 $u$ 和 $v$ 不连通，则 $V^{'}$ 被称作 $u$ 到 $v$ 的点割集。 $u$ 到 $v$ 的最小点割集的大小被称作 $u$ 到 $v$ 的 局部点连通度 (local connectivity)，记作 $κ (u, v)$ 。

还可以在边上作类似的定义：

对于连通图 $G = (V, E)$ ，若 $E^{'} \subseteq E$ 且 $G^{'} = (V, E ∖ E^{'})$ （即从 $G$ 中删去 $E^{'}$ 中的边）不是连通图，则 $E^{'}$ 是图 $G$ 的一个 边割集 (edge cut)。大小为一的边割集又被称作 桥 (bridge)。

对于连通图 $G = (V, E)$ 和整数 $k$ ，若 $G$ 不存在大小为 $k - 1$ 的边割集，则称图 $G$ 是 $k$ - 边连通的 ( $k$ -edge-connected)，而使得上式成立的最大的 $k$ 被称作图 $G$ 的 边连通度 (edge connectivity)，记作 $λ (G)$ 。（对于任何图，边连通度即为最小边割集的大小。）

对于图 $G = (V, E)$ 以及 $u, v \in V$ 满足 $u \neq v$ ， $u$ 可达 $v$ ，若 $E^{'} \subseteq E$ ，且在 $G^{'} = (V, E ∖ E^{'})$ 中 $u$ 和 $v$ 不连通，则 $E^{'}$ 被称作 $u$ 到 $v$ 的边割集。 $u$ 到 $v$ 的最小边割集的大小被称作 $u$ 到 $v$ 的 局部边连通度 (local edge-connectivity)，记作 $λ (u, v)$ 。

点双连通 (biconnected) 几乎与 $2$ - 点连通完全一致，除了一条边连接两个点构成的图，它是点双连通的，但不是 $2$ - 点连通的。换句话说，没有割点的连通图是点双连通的。

边双连通 ( $2$ -edge-connected) 与 $2$ - 边双连通完全一致。换句话说，没有桥的连通图是边双连通的。

与连通分量类似，也有 点双连通分量 (biconnected component)（极大点双连通子图）和 边双连通分量 ( $2$ -edge-connected component)（极大边双连通子图）。

Whitney 定理：对任意的图 $G$ ，有 $κ (G) \leq λ (G) \leq δ (G)$ 。（不等式中的三项分别为点连通度、边连通度、最小度。）

稀疏图/稠密图

若一张图的边数远小于其点数的平方，那么它是一张 稀疏图 (sparse graph)。

若一张图的边数接近其点数的平方，那么它是一张 稠密图 (dense graph)。

这两个概念并没有严格的定义，一般用于讨论时间复杂度为 $O (| V |^{2})$ 的算法与 $O (| E |)$ 的算法的效率差异（在稠密图上这两种算法效率相当，而在稀疏图上 $O (| E |)$ 的算法效率明显更高）。

补图

对于无向简单图 $G = (V, E)$ ，它的 补图 (complement graph) 指的是这样的一张图：记作 $\bar{G}$ ，满足 $V (\bar{G}) = V (G)$ ，且对任意节点对 $(u, v)$ ， $(u, v) \in E (\bar{G})$ 当且仅当 $(u, v) \notin E (G)$ 。

反图

对于有向图 $G = (V, E)$ ，它的 反图 (transpose graph) 指的是点集不变，每条边反向得到的图，即：若 $G$ 的反图为 $G^{'} = (V, E^{'})$ ，则 $E^{'} = {(v, u) | (u, v) \in E}$ 。

特殊的图

若无向简单图 $G$ 满足任意不同两点间均有边，则称 $G$ 为 完全图 (complete graph)， $n$ 阶完全图记作 $K_{n}$ 。若有向图 $G$ 满足任意不同两点间都有两条方向不同的边，则称 $G$ 为 有向完全图 (complete digraph)。

边集为空的图称为 无边图 (edgeless graph)、空图 (empty graph) 或 零图 (null graph)， $n$ 阶无边图记作 ${\overset{―}{K}}_{n}$ 或 $N_{n}$ 。 $N_{n}$ 与 $K_{n}$ 互为补图。

零图 (null graph) 也可指 零阶图 (order-zero graph) $K_{0}$ ，即点集与边集均为空的图。

若有向简单图 $G$ 满足任意不同两点间都有恰好一条边（单向），则称 $G$ 为 竞赛图 (tournament graph)。

若无向简单图 $G = (V, E)$ 的所有边恰好构成一个圈，则称 $G$ 为 环图/圈图 (cycle graph)， $n$ ( $n \geq 3$ ) 阶圈图记作 $C_{n}$ 。易知，一张图为圈图的充分必要条件是，它是 $2$ - 正则连通图。

若无向简单图 $G = (V, E)$ 满足，存在一个点 $v$ 为支配点，其余点之间没有边相连，则称 $G$ 为 星图/菊花图 (star graph)， $n + 1$ ( $n \geq 1$ ) 阶星图记作 $S_{n}$ 。

若无向简单图 $G = (V, E)$ 满足，存在一个点 $v$ 为支配点，其它点之间构成一个圈，则称 $G$ 为 轮图 (wheel graph)， $n + 1$ ( $n \geq 3$ ) 阶轮图记作 $W_{n}$ 。

若无向简单图 $G = (V, E)$ 的所有边恰好构成一条简单路径，则称 $G$ 为 链 (chain/path graph)， $n$ 阶的链记作 $P_{n}$ 。易知，一条链由一个圈图删去一条边而得。

如果一张无向连通图不含环，则称它是一棵 树 (tree)。

如果一张无向连通图包含恰好一个环，则称它是一棵 基环树 (pseudotree)。

如果一张有向弱连通图每个点的入度都为 $1$ ，则称它是一棵 基环外向树。

如果一张有向弱连通图每个点的出度都为 $1$ ，则称它是一棵 基环内向树。

多棵树可以组成一个 森林 (forest)，多棵基环树可以组成 基环森林 (pseudoforest)，多棵基环外向树可以组成 基环外向树森林，多棵基环内向树可以组成 基环内向森林 (functional graph)。

如果一张无向连通图的每条边最多在一个环内，则称它是一棵 仙人掌 (cactus)。多棵仙人掌可以组成沙漠。

如果一张图的点集可以被分为两部分，每一部分的内部都没有连边，那么这张图是一张 二分图 (bipartite graph)。如果二分图中任何两个不在同一部分的点之间都有连边，那么这张图是一张 完全二分图 (complete bipartite graph/biclique)，一张两部分分别有 $n$ 个点和 $m$ 个点的完全二分图记作 $K_{n, m}$ 。

如果一张图可以画在一个平面上，且没有两条边在非端点处相交，那么这张图是一张 平面图 (planar graph)。一张图的任何子图都不是 $K_{5}$ 或 $K_{3, 3}$ 是其为一张平面图的充要条件。对于简单连通平面图 $G = (V, E)$ 且 $V \geq 3$ ， $| E | \leq 3 | V | - 6$ 。

同构

两个图 $G$ 和 $H$ ，如果存在一个双射 $f : V (G) \to V (H)$ ，且满足 $(u, v) \in E (G)$ ，当且仅当 $(f (u), f (v)) \in E (H)$ ，则我们称 $f$ 为 $G$ 到 $H$ 的一个 同构 (isomorphism)，且图 $G$ 与图 $H$ 是 同构的 (isomorphic)，记作 $G ≅ H$ 。

从定义可知，若 $G ≅ H$ ，必须满足：

$| V (G) | = | V (H) |, | E (G) | = | E (H) |$
$G$ 和 $H$ 结点度的非增序列相同
$G$ 和 $H$ 存在同构的导出子图

无向简单图的二元运算

对于无向简单图，我们可以定义如下二元运算：

交 (intersection)：图 $G = (V_{1}, E_{1}), H = (V_{2}, E_{2})$ 的交定义成图 $G \cap H = (V_{1} \cap V_{2}, E_{1} \cap E_{2})$ 。

容易证明两个无向简单图的交还是无向简单图。

并 (union)：图 $G = (V_{1}, E_{1}), H = (V_{2}, E_{2})$ 的并定义成图 $G \cup H = (V_{1} \cup V_{2}, E_{1} \cup E_{2})$ 。

和 (sum)/直和 (direct sum)：对于 $G = (V_{1}, E_{1}), H = (V_{2}, E_{2})$ ，任意构造 $H^{'} ≅ H$ 使得 $V (H^{'}) \cap V_{1} = \emptyset$ ( $H^{'}$ 可以等于 $H$ )。此时与 $G \cup H^{'}$ 同构的任何图称为 $G$ 和 $H$ 的和/直和/不交并，记作 $G + H$ 或 $G \oplus H$ 。

若 $G$ 与 $H$ 的点集本身不相交，则 $G \cup H = G + H$ 。

比如，森林可以定义成若干棵树的和。

并与和的区别：可以理解为，「并」会让两张图中「名字相同」的点、边合并，而「和」则不会。

特殊的点集/边集

支配集

对于无向图 $G = (V, E)$ ，若 $V^{'} \subseteq V$ 且 $\forall v \in (V ∖ V^{'})$ 存在边 $(u, v) \in E$ 满足 $u \in V^{'}$ ，则 $V^{'}$ 是图 $G$ 的一个 支配集 (dominating set)。

无向图 $G$ 最小的支配集的大小记作 $γ (G)$ 。求一张图的最小支配集是 NP-Hard 的。

对于有向图 $G = (V, E)$ ，若 $V^{'} \subseteq V$ 且 $\forall v \in (V ∖ V^{'})$ 存在边 $(u, v) \in E$ 满足 $u \in V^{'}$ ，则 $V^{'}$ 是图 $G$ 的一个 出 - 支配集 (out-dominating set)。类似地，可以定义有向图的 入 - 支配集 (in-dominating set)。

有向图 $G$ 最小的出 - 支配集大小记作 $γ^{+} (G)$ ，最小的入 - 支配集大小记作 $γ^{-} (G)$ 。

边支配集

对于图 $G = (V, E)$ ，若 $E^{'} \subseteq E$ 且 $\forall e \in (E ∖ E^{'})$ 存在 $E^{'}$ 中的边与其有公共点，则称 $E^{'}$ 是图 $G$ 的一个 边支配集 (edge dominating set)。

求一张图的最小边支配集是 NP-Hard 的。

独立集

对于图 $G = (V, E)$ ，若 $V^{'} \subseteq V$ 且 $V^{'}$ 中任意两点都不相邻，则 $V^{'}$ 是图 $G$ 的一个 独立集 (independent set)。

图 $G$ 最大的独立集的大小记作 $α (G)$ 。求一张图的最大独立集是 NP-Hard 的。

匹配

对于图 $G = (V, E)$ ，若 $E^{'} \in E$ 且 $E^{'}$ 中任意两条不同的边都没有公共的端点，且 $E^{'}$ 中任意一条边都不是自环，则 $E^{'}$ 是图 $G$ 的一个 匹配 (matching)，也可以叫作 边独立集 (independent edge set)。如果一个点是匹配中某条边的一个端点，则称这个点是 被匹配的 (matched)/饱和的 (saturated)，否则称这个点是 不被匹配的 (unmatched)。

边数最多的匹配被称作一张图的 最大匹配 (maximum-cardinality matching)。图 $G$ 的最大匹配的大小记作 $ν (G)$ 。

如果边带权，那么权重之和最大的匹配被称作一张图的 最大权匹配 (maximum-weight matching)。

如果一个匹配在加入任何一条边后都不再是一个匹配，那么这个匹配是一个 极大匹配 (maximal matching)。最大的极大匹配就是最大匹配，任何最大匹配都是极大匹配。极大匹配一定是边支配集，但边支配集不一定是匹配。最小极大匹配和最小边支配集大小相等，但最小边支配集不一定是匹配。求最小极大匹配是 NP 困难的。

如果在一个匹配中所有点都是被匹配的，那么这个匹配是一个 完美匹配 (perfect matching)。如果在一个匹配中只有一个点不被匹配，那么这个匹配是一个 准完美匹配 (near-perfect matching)。

求一张普通图或二分图的匹配或完美匹配个数都是**#P完全(Sharp-P Complete)**的。

对于一个匹配 $M$ ，若一条路径以非匹配点为起点，每相邻两条边的其中一条在匹配中而另一条不在匹配中，则这条路径被称作一条 交替路径 (alternating path)；一条在非匹配点终止的交替路径，被称作一条 增广路径 (augmenting path)。

托特定理： $n$ 阶无向图 $G$ 有完美匹配当且仅当对于任意的 $V^{'} \subset V (G)$ ， $p_{odd} (G - V^{'}) \leq | V^{'} |$ ，其中 $p_{odd}$ 表示奇数阶连通分支数。

托特定理（推论）：任何无桥 3 - 正则图都有完美匹配。

点覆盖

对于图 $G = (V, E)$ ，若 $V^{'} \subseteq V$ 且 $\forall e \in E$ 满足 $e$ 的至少一个端点在 $V^{'}$ 中，则称 $V^{'}$ 是图 $G$ 的一个 点覆盖 (vertex cover)。

点覆盖集必为支配集，但极小点覆盖集不一定是极小支配集。

一个点集是点覆盖的充要条件是其补集是独立集，因此最小点覆盖的补集是最大独立集。求一张图的最小点覆盖是 NP-Hard 的。

一张图的任何一个匹配的大小都不超过其任何一个点覆盖的大小。完全二分图 $K_{n, m}$ 的最大匹配和最小点覆盖大小都为 $min (n, m)$ 。

边覆盖

对于图 $G = (V, E)$ ，若 $E^{'} \subseteq E$ 且 $\forall v \in V$ 满足 $v$ 与 $E^{'}$ 中的至少一条边相邻，则称 $E^{'}$ 是图 $G$ 的一个 边覆盖 (edge cover)。

最小边覆盖的大小记作 $ρ (G)$ ，可以由最大匹配贪心扩展求得：对于所有非匹配点，将其一条邻边加入最大匹配中，即得到了一个最小边覆盖。

最大匹配也可以由最小边覆盖求得：对于最小边覆盖中每对有公共点的边删去其中一条。

一张图的最小边覆盖的大小加上最大匹配的大小等于图的点数，即 $ρ (G) + ν (G) = | V (G) |$ 。

一张图的最大匹配的大小不超过最小边覆盖的大小，即 $ν (G) \leq ρ (G)$ 。特别地，完美匹配一定是一个最小边覆盖，这也是上式取到等号的唯一情况。

一张图的任何一个独立集的大小都不超过其任何一个边覆盖的大小。完全二分图 $K_{n, m}$ 的最大独立集和最小边覆盖大小都为 $max (n, m)$ 。

团

对于图 $G = (V, E)$ ，若 $V^{'} \subseteq V$ 且 $V^{'}$ 中任意两个不同的顶点都相邻，则 $V^{'}$ 是图 $G$ 的一个 团 (clique)。团的导出子图是完全图。

如果一个团在加入任何一个顶点后都不再是一个团，则这个团是一个 极大团 (maximal clique)。

一张图的最大团的大小记作 $ω (G)$ ，最大团的大小等于其补图最大独立集的大小，即 $ω (G) = α (\bar{G})$ 。求一张图的最大团是 NP-hard 的。

图的存储

对图进行操作，就需要进行图的存储。在本文中，用 $n$ 代指图的点数，用 $m$ 代指图的边数，用 $d^{+} (u)$ 代指点 $u$ 的出度，即以 $u$ 为出发点的边数。

直接存边

方法

使用一个数组来存边，数组中的每个元素都包含一条边的起点与终点（带边权的图还包含边权）。（或者使用多个数组分别存起点，终点和边权。）

代码实现

c++

struct Edge {int u, v;};
int n, m;
vector<Edge> e;
vector<bool> vis;
bool find_edge(int u, int v) {
  for (int i = 1; i <= m; ++i) {
    if (e[i].u == u && e[i].v == v) {
      return true;
    }
  }
  return false;
}

void dfs(int u) {
  if (vis[u]) return;
  vis[u] = true;
  for (int i = 1; i <= m; ++i) {
    if (e[i].u == u) {
      dfs(e[i].v);
    }
  }
}

int main() {
  cin >> n >> m;
  vis.resize(n + 1, false);//resize()函数，第一个参数是更改的大小，第二个参数(可选)
  e.resize(m + 1);//是填充的值，如果没有，就使用构造函数或默认
  for (int i = 1; i <= m; ++i) cin >> e[i].u >> e[i].v;

  return 0;
}

复杂度

查询是否存在某条边： $O (m)$ 。遍历一个点的所有出边： $O (m)$ 。遍历整张图： $O (n m)$ 。空间复杂度： $O (m)$ 。

应用

由于直接存边的遍历效率低下，一般不用于遍历图。

在 Kruskal 算法中，由于需要将边按边权排序，需要直接存边。

在有的题目中，需要多次建图（如建一遍原图，建一遍反图），此时既可以使用多个其它数据结构来同时存储多张图，也可以将边直接存下来，需要重新建图时利用直接存下的边来建图。

关联矩阵

考虑一个n列e行的二维数组inc[][]。这里，n是点的个数，而e是边的条数。如果存在从u到v的边e，则inc[u][e]=inc[v][e]=1。不难发现，对于其中的每一列，只会有两个值为1，而其他的值为0。
该方法在某些特定问题上十分有效，但是由于其对数组的利用率不高，因此不过多介绍。

邻接矩阵

方法

使用一个二维数组 adj 来存边，其中 adj[u][v] 为 1 表示存在 $u$ 到 $v$ 的边，为 0 表示不存在。如果是带边权的图，可以对上述的定义进行扩展，在 adj[u][v] 中存储 $u$ 到 $v$ 的边的边权。（这里，对于无向图我们可以使用整个数组，也可以使用整个数组对角线的一半；而对于有向图和带权图，我们要使用整个数组。）
注意：如果不考虑自环，则所有的adj[i][i]，不论在无权图或带权图中，都不存在。对于不存在的边，通常统一取值为 $\infty$ 或0。

代码实现

cpp

#include <iostream>
#include <vector>

using namespace std;

int n, m;
vector<bool> vis;
vector<vector<bool> > adj;

bool find_edge(int u, int v) { return adj[u][v]; }

void dfs(int u) {
  if (vis[u]) return;
  vis[u] = true;
  for (int v = 1; v <= n; ++v) {
    if (adj[u][v]) {
      dfs(v);
    }
  }
}

int main() {
  cin >> n >> m;

  vis.resize(n + 1, false);
  adj.resize(n + 1, vector<bool>(n + 1, false));

  for (int i = 1; i <= m; ++i) {
    int u, v;
    cin >> u >> v;
    adj[u][v] = true;
  }

  return 0;
}

复杂度

查询是否存在某条边： $O (1)$ 。遍历一个点的所有出边： $O (n)$ 。
遍历整张图： $O (n^{2})$ 。空间复杂度： $O (n^{2})$ 。（一般情况下很难达到，这是比较大的浪费）

应用

邻接矩阵只适用于没有重边（或重边可以忽略）的情况。

其最显著的优点是可以 $O (1)$ 查询一条边是否存在。（这是邻接表无法做到的。）

由于邻接矩阵在稀疏图上效率很低（尤其是在点数较多的图上，空间无法承受），所以一般只会在稠密图上使用邻接矩阵。

点操作和边操作

（来自数据结构(上) - 清华大学 - 学堂在线 (xuetangx.com)）

点操作

如果我们想要实现一个“对于任意顶点i，如何枚举其所有的邻接顶点neighbor？”的问题，对于邻接矩阵来说，是这样实现的：

c++

int nextNbr(int i, int j){//点操作
    while(-1 < j && !exists(i,--j));
    return j; 
}
//初始时，传入nextNbr(i,n)；

bool exists(int i, int j){//边操作
    return ( 0 <= i ) && ( i < n ) && ( 0 <= j ) && ( j < n ) && E[i][j] != NULL;
}

如果，使用邻接表的话，时间复杂度可以降低至 $O (1 + d^{-} (i))$ 。

如果要进行更为复杂的操作，如点的插入算法和点的删除算法，这时候的情况就要比边的插入或删除算法更加复杂，因为在边的插入和删除算法中，矩阵的规模没有发生变动；而在点的插入和删除算法中，边的规模可能会发生变动。
对于点的插入，如果现在有一个点集v[]和一个邻接矩阵E[][]，我们需要插入一个新的点i，则发生的变化是：
1. 对每一个行向量的末尾增加一个单元并引入一个初始为空的记录，并且更新边的计数。
2. 生成一个行向量，长度为n+1，并且每一个元素都初始化为空。
3. 取出新增加的行向量的地址，并放入更上一级的边表中，以便于后续的操作。
4. 插入点i至点集v[]的末尾。
对于点的删除，和点的插入算法类似。

边操作

当然，处理这些点操作之外，还有边操作，如返回e(u,v)的数据、状态、权重等。这些内容都需要先进行exists(u,v)判断。
如果进行更加复杂的操作呢？如边的插入算法和边的删除算法：
对于边的插入算法：
1. 忽略已有的边（使用exists(u,v)进行判断）；
2. 创建新的边（new Edge()），并更新边的计数；
3. 更新关联顶点的出度和入度。（增加）
对于边的删除算法：
1. 备份边(u,v)的数据；
2. 删除边(u,v)，并更新边的计数；
3. 更新关联顶点的出度和入度。
4. 返回被删除边的信息。（减少）

邻接表

方法

使用一个支持动态增加元素的数据结构构成的数组，如 vector<int> adj[n + 1] 来存边，其中 adj[u] 存储的是点 $u$ 的所有出边的相关信息（终点、边权等）。

代码

cpp

#include <iostream>
#include <vector>

using namespace std;

int n, m;
vector<bool> vis;
vector<vector<int> > adj;

bool find_edge(int u, int v) {
  for (int i = 0; i < adj[u].size(); ++i) {
    if (adj[u][i] == v) {
      return true;
    }
  }
  return false;
}

void dfs(int u) {
  if (vis[u]) return;
  vis[u] = true;
  for (int i = 0; i < adj[u].size(); ++i) dfs(adj[u][i]);
}

int main() {
  cin >> n >> m;

  vis.resize(n + 1, false);
  adj.resize(n + 1);

  for (int i = 1; i <= m; ++i) {
    int u, v;
    cin >> u >> v;
    adj[u].push_back(v);
  }

  return 0;
}

基于链表的邻接表

当然，也可以使用一系列的链表来实现上述操作。

对于有向图 $G = (V, E)$ ，我们需要一共 $V$ 组链表来存放所有的值。
节点包含两个元素：该节点的编号和指向下一个节点的指针。
对于图中的顶点 $v$ ，该条链表的首节点为自己，其余节点为一系列和 $v$ 相连的节点，故邻接表的长度为 $L = 1 + d^{+} (v)$ （不含末尾节点所指向的空节点）。
若图是无向图，则对于一对使用无向边连接而成的两个节点 $(u, v)$ ，它们中间的连接关系要在这一系列的链表中出现两次。具体来说：在第 $u$ 条链表中，要写u->v；而在第 $v$ 条链表中，要写v->u。
若图是带权图，则需要在节点中加入一个权值元素。

复杂度

查询是否存在 $u$ 到 $v$ 的边： $O (d^{+} (u))$ （如果事先进行了排序就可以使用二分查找做到 $O (\log (d^{+} (u)))$ ）。

遍历点 $u$ 的所有出边： $O (d^{+} (u))$ 。

遍历整张图： $O (n + m)$ 。空间复杂度： $O (m)$ 。

应用

存各种图都很适合，除非有特殊需求（如需要快速查询一条边是否存在，且点数较少，可以使用邻接矩阵）。

尤其适用于需要对一个点的所有出边进行排序的场合。

链式前向星

百度百科：如果说邻接表是不好写但效率好，邻接矩阵是好写但效率低的话，前向星就是一个相对中庸的数据结构。前向星固然好写，但效率并不高。而在优化为链式前向星后，效率也得到了较大的提升。虽然说，世界上对链式前向星的使用并不是很广泛，但在不愿意写复杂的邻接表的情况下，链式前向星也是一个很优秀的数据结构。

引入

链式前向星其实就是静态建立的邻接表，时间效率为 $O (m)$ ，空间效率为 $O (m)$ ，遍历的效率仍为 $O (m)$ 。链式前向星存储的是以 $[1, n]$ 为起点的边的集合。

例子：对于下面的图 $G = (V, E)$ ，数据由三部分构成：from, to, edgeValue。

bash

链式前向星的输出如下：

bash

1 //以1为起点的边的集合
1 5 6
1 3 4
1 2 1
 
2 //以2为起点的边的集合
2 3 2
 
3 //以3为起点的边的集合
3 4 3
 
4  //以4为起点的边的集合
4 5 7
4 1 5
 
5 //以5为起点的边不存在

语义约定

首先，对所有的边进行标号 $[0, n - 1]$ ，并约定如下变量含义：

next：表示与这个边起点相同的上一条边的编号。
head[i]：表示以 i 为起点的最后一条边的编号，初始化为-1。

然后写增加边的函数：

cpp

void add_edge(int u, int v, int w)//加边，u起点，v终点，w边权
{
    edge[cnt].to = v; //终点
    edge[cnt].w = w; //权值
    edge[cnt].next = head[u];//以u为起点上一条边的编号，也就是与这个边起点相同的上一条边的编号
    head[u] = cnt++;//更新以u为起点上一条边的编号
}

例如：对于1 3 4这条边，有：edge[3].to = 3; edge[3].next = 0; head[1] = 3;。

遍历函数如下：

cpp

for(int i = 1; i <= n; i++)//n个起点
{
    cout << i << endl;
    for(int j = head[i]; j != -1; j = edge[j].next){//遍历以i为起点的边
        cout << i << " " << edge[j].to << " " << edge[j].w << endl;
    }
    cout << endl;
}

第一层循环：找出所有的点。依次遍历以 $[1, n]$ 为起点的边的集合。
第二层循环：遍历以i为起点的所有边。
- k首先等于head[i]。其中，head[i]中存的是以 i 为起点的最后一条边的编号。
- 然后通过edge[j].next来找下一条边的编号。
- 当找到最后一个边时（以i为起点的第一条边），由于之前初始化时，head[i]=-1，此时，有：edge[j].next=-1。遍历中止。
代码如下：

cpp

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1005;//点数最大值
int n, m, cnt;//n个点，m条边
struct Edge
{
    int to, w, next;//终点，边权，同起点的上一条边的编号
}edge[maxn];//边集
int head[maxn];//head[i],表示以i为起点的第一条边在边集数组的位置（编号）
void init()//初始化
{
    for (int i = 0; i <= n; i++) head[i] = -1;
    cnt = 0;
}
void add_edge(int u, int v, int w)//加边，u起点，v终点，w边权
{
    edge[cnt].to = v; //终点
    edge[cnt].w = w; //权值
    edge[cnt].next = head[u];//以u为起点上一条边的编号，也就是与这个边起点相同的上一条边的编号
    head[u] = cnt++;//更新以u为起点上一条边的编号
}
int main()
{
    cin >> n >> m;
    int u, v, w;
    init();//初始化
    for (int i = 1; i <= m; i++)//输入m条边
    {
        cin >> u >> v >> w;
        add_edge(u, v, w);//加边
        /*
        加双向边
        add_edge(u, v, w);
        add_edge(v, u, w);
        */
    }
    for (int i = 1; i <= n; i++)//n个起点
    {
        cout << i << endl;
        for (int j = head[i]; j != -1; j = edge[j].next)//遍历以i为起点的边
        {
            cout << i << " " << edge[j].to << " " << edge[j].w << endl;
        }
        cout << endl;
    }
    return 0;
}

时间复杂度总结

Method	Edge List	Adjacent List	Adjacent Map	Adj Matrix
`numVertices()`	$O (1)$	$O (1)$	$O (1)$	$O (1)$
`numEdges()`	$O (1)$	$O (1)$	$O (1)$	$O (1)$
`vertices()`	$O (n)$	$O (n)$	$O (n)$	$O (n)$
`edges()`	$O (m)$	$O (m)$	$O (m)$	$O (m)$
`getEdge(u, v)`	$O (m)$	$O (min (d_{u}, d_{v}))$	期望 $O (1)$	$O (1)$
`inDegree(v)`	$O (m)$	$O (1)$	$O (1)$	$O (n)$
`outDegree(v)`	$O (m)$	$O (1)$	$O (1)$	$O (n)$
`outgoingEdges(v)`	$O (m)$	$O (d_{v})$	$O (d_{v})$	$O (n)$
`incomingEdges(v)`	$O (m)$	$O (d_{v})$	$O (d_{v})$	$O (n)$
`insertVertex(x)`	$O (1)$	$O (1)$	$O (1)$	$O (n^{2})$
`removeVertex(v)`	$O (m)$	$O (d_{v})$	$O (d_{v})$	$O (n^{2})$
`insertEdge(u, v, x)`	$O (1)$	$O (1)$	期望 $O (1)$	$O (1)$
`removeEdge(e)`	$O (1)$	$O (1)$	期望 $O (1)$	$O (1)$

参考资料

数据结构(上) - 清华大学 - 学堂在线 (xuetangx.com)

平面图的欧拉定理 - chasedeath - 博客园 (cnblogs.com)

联通平面图的欧拉公式及推广(联通的推广需要用到平面次数和等于边数的两倍)_区域的数量v+e-CSDN博客

欧拉公式_平面图的欧拉公式-CSDN博客

图的存储 - OI Wiki (oi-wiki.org)

平面图

定义

如果图 $G$ 能画在平面 $S$ 上，即除顶点处外无边相交，则称 $G$ 可平面嵌入 $S$ ， $G$ 为可平面图或平面图。画出的没有边相交的图称为 $G$ 的平面表示或平面嵌入。

性质

设 $G$ 是平面图，由 $G$ 的边将 $G$ 所在的平面划分成若干个区域，每个区域称为 $G$ 的一个面，其中面积无限的面称为无限面或外部面，面积有限的称为有限面或内部面。
包围每个面的所有边组成的回路称为该面的边界。一个面 $F$ 的边界中含有的边数（割边计算2次）称为面 $F$ 的次数，记为 $d (f)$ 。
对于这个图来说，有： $d (f_{i}) = {1, 3, 6, 6}, i \in [1, 4]$ 。

Jordan曲线定理

Jordan曲线：一条连续的、自身不交的、起点和终点重合的封闭曲线称为Jordan曲线。
Jordan曲线定理：平面上的任意一条Jordan曲线将平面分成两个区域，一个有限区域（内部区域）和一个无限区域（外部区域）。其中，内部和外部均为开集。并且，如果在这两个区域内分别取一点，再用一条曲线（这里不是Jordan曲线）将其相连，则这条连线必定和原来的闭合Jordan曲线相交。

平面图的次数公式

（定理）设 $G = (V, E)$ 是平面图， $F$ 是平面图的面数，则有

\sum_{f \in F} d (f) = 2 E .

即：平面图的所有面的次数之和等于边数的两倍。

证明：对 $G$ 的任意一条边 $e$ ，如果 $e$ 是某一个面的割边，那么，根据定义，该边给 $G$ 的总次数贡献两次；如果 $e$ 不是某一个面的割边，那么，它必然是两个面的公共边。所以，由面的次数的定义， $e$ 也给 $G$ 的总次数贡献了两次。

欧拉定理

多面体欧拉定理：在一凸多面体中，顶点数-棱边数+面数=2，即 $V - E + F = 2$ 。

平面几何中的欧拉定理：对于任意一个平面图（或称为平面图形），有

V - E + R - C = 1

其中， $V$ 表示图形的顶点数（Vertices）， $E$ 表示图形的边数（Edges）， $R$ 表示图形域的个数（Ranges）， $C$ 表示连通块的数量（Connected Blocks）。

特别地，如果该平面图是连通图，则有 $K = 1$ ，上式就被改写为 $V - E + R = 2$ 。这里， $R$ 就是该平面图 $G$ 的面数 $F$ 。（推论）设 $G$ 是具有 $V$ 个点， $E$ 条边， $F$ 个面的连通平面图，如果对 $G$ 的每个面 $f$ ，有 $d (f) \geq l \geq 3$ ，则有

E \leq \frac{l}{l - 2} (V - 2) .

设图中围成一个面最少需要 $L$ 个边，即 $2 E \geq L \cdot R$ ，则对于连通的平面图，有：

E \leq {\begin{cases} L \cdot \frac{V - 2}{L - 2}, & if L \geq 3, \\ 3 V - 6, & if L = 3. \end{cases}

对于非连通图来说，以上的 $C$ 个式子相加。不难发现，当 $C = 1, L = 3$ 时取得最大值，即 $E \leq 3 V - 6$ 恒成立。

所以， $E \leq O (n) ≪ O (n^{2})$ ，空间的利用率仅有 $\frac{1}{n}$ 。

例子

K5的非平面性

$E = 10, V = 5, E > 3 V - 6$ 。

或考虑：在 $K_{5}$ 中，一个面最多平均对应 $\frac{3}{2}$ 条边。

K3,3的非平面性

$K_{3, 3}$ 是二部图，无奇圈，所以， $l$ 至少为4。所以， $\frac{l}{l - 2} (n - 2) = 8$ 。而 $V = 9$ .

参考资料

平面图_面的次数之和等于边数的二倍-CSDN博客

深度优先搜索

引入

深度优先搜索(Depth First Search, DFS)是一种用于遍历或搜索树或图的算法。
算法的思想是：沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所在边都已被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。

特征

DFS 最显著的特征在于其 递归调用自身。DFS 会对其访问过的点打上访问标记，在遍历图时跳过已打过标记的点，以确保 每个点仅访问一次。符合以上两条规则的函数，便是广义上的 DFS。
DFS的大致结构如下：实际的 DFS 会在以上代码基础上加入一些代码，利用 DFS 性质进行其他操作。

cpp

void DFS(v){
    visit(v);
    for(node u: adj[v]){
        if(!visit(u)){
            DFS(u);
            //在有些情况下，可能会回溯
        }
    }
}

时间复杂度

该算法通常的时间复杂度为 $O (n + m)$ ，空间复杂度为 $O (n)$ ，其中 $n$ 表示点数， $m$ 表示边数。注意空间复杂度包含了栈空间，栈空间的空间复杂度是 $O (n)$ 的。在平均 $O (1)$ 遍历一条边的条件下才能达到此时间复杂度，例如用前向星或邻接表存储图；如果用邻接矩阵则不一定能达到此复杂度。

实现

栈实现

DFS可以使用栈为遍历中的暂存容器来实现，而BFS可以使用队列为遍历中的暂存容器。

cpp

vector<vector<int>> adj;  // 邻接表
vector<bool> vis;         // 记录节点是否已经遍历

void dfs(int s) {
  stack<int> st;
  st.push(s);
  vis[s] = true;

  while (!st.empty()) {
    int u = st.top();
    st.pop();

    for (int v : adj[u]) {
      if (!vis[v]) {
        vis[v] = true;  // 确保栈里没有重复元素
        st.push(v);
      }
    }
  }
}

递归实现

函数在递归调用时的求值如同对栈的添加和删除元素的顺序，故函数调用所占据的虚拟地址被称为函数调用栈（Call Stack），DFS 可用递归的方式实现。

邻接表

cpp

vector<vector<int>> adj;  // 邻接表
vector<bool> vis;         // 记录节点是否已经遍历

void dfs(const int u) {
  vis[u] = true;
  for (int v : adj[u])
    if (!vis[v]) dfs(v)
}

链式前向星

Java

public void dfs(int u) {
    vis[u] = true;
    for (int i = head[u]; i != 0; i = e[i].x) {
        if (!vis[e[i].t]) {
            dfs(v);
        }
    }
}

DFS 序列

DFS 序列是指 DFS 调用过程中访问的节点编号的序列。

我们发现，每个子树都对应 DFS 序列中的连续一段（一段区间）。

括号序列

DFS 进入某个节点的时候记录一个左括号 (，退出某个节点的时候记录一个右括号 )。

每个节点会出现两次。相邻两个节点的深度相差 1。

一般图上 DFS

对于非连通图，只能访问到起点所在的连通分量。

对于连通图，DFS 序列通常不唯一。

注：树的 DFS 序列也是不唯一的。

在 DFS 过程中，通过记录每个节点从哪个点访问而来，可以建立一个树结构，称为 DFS 树。DFS 树是原图的一个生成树。其有很多性质，比如可以用来求强连通分量。

广度优先搜索

引入

广度优先搜索（宽度优先搜索）(Breadth First Search, BFS)也是一种用于遍历或搜索树或图的算法。
算法的思想是：广度优先。就是每次都尝试访问同一层的节点。如果同一层都访问完了，再访问下一层。这样做的结果是，BFS 算法找到的路径是从起点开始的最短合法路径。换言之，这条路径所包含的边数最小。在 BFS 结束时，每个节点都是通过从起点到该点的最短路径访问的。

代码实现

text

bfs(s) {
  q = new queue()
  q.push(s), visited[s] = true
  while (!q.empty()) {
    u = q.pop()
    for each edge(u, v) {
      if (!visited[v]) {
        q.push(v)
        visited[v] = true
      }
    }
  }
}

cpp

//c++版本，使用队列，使用链式前向星进行图的存储。
void bfs(int u) {
  while (!Q.empty()) Q.pop();
  Q.push(u);
  vis[u] = 1;
  d[u] = 0;
  p[u] = -1;
  while (!Q.empty()) {
    u = Q.front();
    Q.pop();
    for (int i = head[u]; i; i = e[i].nxt) {
      if (!vis[e[i].to]) {
        Q.push(e[i].to);
        vis[e[i].to] = 1;
        d[e[i].to] = d[u] + 1;
        p[e[i].to] = u;
      }
    }
  }
}

void restore(int x) {
  vector<int> res;
  for (int v = x; v != -1; v = p[v]) {
    res.push_back(v);
  }
  std::reverse(res.begin(), res.end());
  for (int i = 0; i < res.size(); ++i) printf("%d", res[i]);
  puts("");
}

具体来说，我们用一个队列 Q 来记录要处理的节点，然后开一个布尔数组 vis[] 来标记是否已经访问过某个节点。

开始的时候，我们将所有节点的 vis 值设为 0，表示没有访问过；然后把起点 s 放入队列 Q 中并将 vis[s] 设为 1。

之后，我们每次从队列 Q 中取出队首的节点 u，然后把与 u 相邻的所有节点 v 标记为已访问过并放入队列 Q。

循环直至当队列 Q 为空，表示 BFS 结束。

在 BFS 的过程中，也可以记录一些额外的信息。例如上述代码中，d 数组用于记录起点到某个节点的最短距离（要经过的最少边数），p 数组记录是从哪个节点走到当前节点的。

有了 d 数组，可以方便地得到起点到一个节点的距离。

有了 p 数组，可以方便地还原出起点到一个点的最短路径。上述代码中的 restore 函数使用该数组依次输出从起点到节点 x 的最短路径所经过的节点。

时间复杂度 $O (n + m)$

空间复杂度 $O (n)$ （vis 数组和队列）

open-closed 表

在实现 BFS 的时候，本质上我们把未被访问过的节点放在一个称为 open 的容器中，而把已经访问过了的节点放在一个称为 closed 容器中。

在树/图上 BFS

BFS 序列

类似 DFS 序列，BFS 序列是指在 BFS 过程中访问的节点编号的序列。

一般图上 BFS

如果原图不连通，只能访问到从起点出发能够到达的点。

BFS 序列通常也不唯一。

类似的我们也可以定义 BFS 树：在 BFS 过程中，通过记录每个节点从哪个点访问而来，可以建立一个树结构，即为 BFS 树。

应用

在一个无权图上求从起点到其他所有点的最短路径。
在 $O (n + m)$ 时间内求出所有连通块。（我们只需要从每个没有被访问过的节点开始做 BFS，显然每次 BFS 会走完一个连通块）
如果把一个游戏的动作看做是状态图上的一条边（一个转移），那么 BFS 可以用来找到在游戏中从一个状态到达另一个状态所需要的最小步骤。
在一个有向无权图中找最小环。（从每个点开始 BFS，在我们即将抵达一个之前访问过的点开始的时候，就知道遇到了一个环。图的最小环是每次 BFS 得到的最小环的平均值。）
找到一定在 $(a, b)$ 最短路上的边。（分别从 a 和 b 进行 BFS，得到两个 d 数组。之后对每一条边 $(u, v)$ ，如果 $d_{a} [u] + 1 + d_{b} [v] = d_{a} [b]$ ，则说明该边在最短路上）
找到一定在 $(a, b)$ 最短路上的点。（分别从 a 和 b 进行 BFS，得到两个 d 数组。之后对每一个点 v，如果 $d_{a} [v] + d_{b} [v] = d_{a} [b]$ ，则说明该点在某条最短路上）
找到一条长度为偶数的最短路。（我们需要一个构造一个新图，把每个点拆成两个新点，原图的边 $(u, v)$ 变成 $((u, 0), (v, 1))$ 和 $((u, 1), (v, 0))$ 。对新图做 BFS， $(s, 0)$ 和 $(t, 0)$ 之间的最短路即为所求）
在一个边权为 0/1 的图上求最短路，见下方双端队列 BFS。

双端队列 BFS

双端队列 BFS 又称 0-1 BFS。（使用双向列表deque）

适用范围

边权值为可能有，也可能没有（由于 BFS 适用于权值为 1 的图，所以一般权值是 0 或 1），或者能够转化为这种边权值的最短路问题。

例如在走迷宫问题中，你可以花 1 个金币走 5 步，也可以不花金币走 1 步，这就可以用 0-1 BFS 解决。

实现

一般情况下，我们把没有权值的边扩展到的点放到队首，有权值的边扩展到的点放到队尾。这样即可保证像普通 BFS 一样整个队列队首到队尾权值单调不下降。

下面是伪代码：

cpp

while (队列不为空) {
  int u = 队首;
  弹出队首;
  for (枚举 u 的邻居) {
    更新数据
    if (...)
      添加到队首;
    else
      添加到队尾;
  }
}

拓扑排序

定义

在图论中，**拓扑排序(Topological Sorting)是一个有向无环图(Directed Acyclic Graph, DAG)**的所有顶点的线性序列，且该序列必须满足下面两个条件：

每个顶点出现且只出现一次。
若存在一条从顶点 A 到顶点 B 的路径，那么在序列中顶点 A 出现在顶点 B 的前面。

注意：有向无环图（DAG）才有拓扑排序，非DAG图没有拓扑排序一说。

例子：对于下面的图来说，一个可能的拓扑排序可以是[1,3,2,4,5,6,7,8]。拓扑排序的结果不唯一。

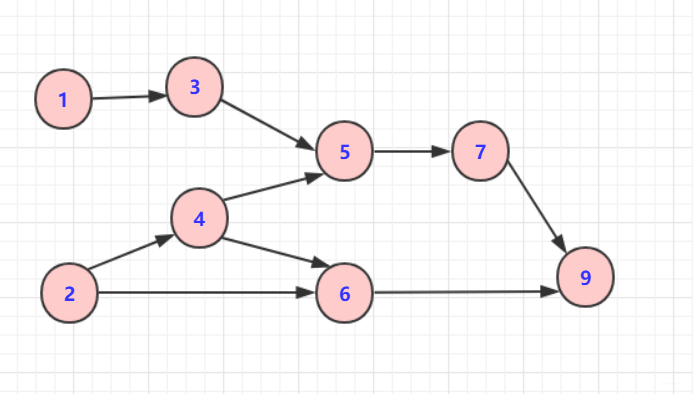
实现：零入度算法

零入度算法，又称作Kahn算法，是使用BFS实现的拓扑排序的算法。

算法思路

从 DAG 图中找到入度为 0 的节点 A（也就是没有箭头指向它的节点），将其放入拓扑序列的结果集。
同时删除由节点 A 出发的所有边。
在剩下的 DAG 图中重复 1-2 两步。
如果最后可以把全部的节点都删除并加入到结果集，那表示 DAG 图可以被拓扑排序；否则，如果最后有节点被剩下，那说明该图是有环图，无法被拓扑排序。

代码的核心是维持一个入度为 0 的顶点的集合。

代码实现

伪代码：

text

L ← Empty list that will contain the sorted elements
S ← Set of all nodes with no incoming edges
while S is not empty do
    remove a node n from S
    insert n into L
    for each node m with an edge e from n to m do
        remove edge e from the graph
        if m has no other incoming edges then
            insert m into S
if graph has edges then
    return error (graph has at least one cycle)
else
    return L (a topologically sorted order)

具体代码：

cpp

int n, m;
vector<int> G[MAXN];
int in[MAXN];  // 存储每个结点的入度

bool toposort() {
  vector<int> L;
  queue<int> S;
  for (int i = 1; i <= n; i++)
    if (in[i] == 0) S.push(i);
  while (!S.empty()) {
    int u = S.front();
    S.pop();
    L.push_back(u);
    for (auto v : G[u]) {
      if (--in[v] == 0) {
        S.push(v);
      }
    }
  }
  if (L.size() == n) {
    for (auto i : L) cout << i << ' ';
    return true;
  } else {
    return false;
  }
}

复杂度

假设这个图 $G = (V, E)$ 在初始化入度为0的集合 $S$ 的时候就需要遍历整个图，并检查每一条边，因而有 $O (E + V)$ 的复杂度。然后对该集合进行操作，显然也是需要 $O (E + V)$ 的时间复杂度。

因而总的时间复杂度就有 $O (E + V)$ 。

实现：零出度算法

零出度算法，是一种使用DFS实现的拓扑排序的算法，在这里，它可以看作是Kahn算法的逆向思路。

思路

选取图中任意一个节点 A，将其状态标记为 “搜索中”
寻找节点 A 的邻接点（沿着箭头指向寻找相邻的节点）
1. 如果 A 存在邻接点
  1. 如果 A 的邻接点中存在状态为 “搜索中” 的邻接点，那么表示 DAG 图有环路，不可拓扑排序。
  2. 否则，那么任意选择一个状态为 “未搜索” 的邻接点 B，使用递归对 B 重复做 1 和 2 操作，注意此时 B 的邻接点判断不包含来路（也就是 A 节点）。等到 A 的所有邻接点都被搜索到，递归回溯回 A 节点的时候，那么 A 节点也会被标记为 “已搜索”，并压入结果栈。
2. 如果 A 不存在邻接点，那么将节点 A 的状态改为 “已完成”，并且将其压入一个结果集的栈中。
A 节点及其相邻节点都搜索完毕后，如果还有未搜索的节点，那么任意选取一个节点当做出发点，继续重复 1,2,3 步骤。
直到所有的节点都被搜索并压入栈，那么此时结果栈中，从栈顶到栈底的顺序，就是拓扑排序的顺序。

代码实现

cpp

using Graph = vector<vector<int>>;  // 邻接表

struct TopoSort {
  enum class Status : uint8_t { to_visit, visiting, visited };

  const Graph& graph;
  const int n;
  vector<Status> status;
  vector<int> order;
  vector<int>::reverse_iterator it;

  TopoSort(const Graph& graph)
      : graph(graph),
        n(graph.size()),
        status(n, Status::to_visit),
        order(n),
        it(order.rbegin()) {}

  bool sort() {
    for (int i = 0; i < n; ++i) {
      if (status[i] == Status::to_visit && !dfs(i)) return false;
    }
    return true;
  }

  bool dfs(const int u) {
    status[u] = Status::visiting;
    for (const int v : graph[u]) {
      if (status[v] == Status::visiting) return false;
      if (status[v] == Status::to_visit && !dfs(v)) return false;
    }
    status[u] = Status::visited;
    *it++ = u;
    return true;
  }
};

复杂度

时间复杂度： $O (E + V)$ ；空间复杂度： $O (V)$ 。

算法优化

对于零入度算法：
如果有时候，我们只需要知道某个 DAG 图是否可以拓扑排序，而不需要真正得到拓扑排序后的结果，那么可以不需要结果集列表，只需要统计被删除的节点的数量即可，如果该数量等于 DAG 图的节点数，那么 DAG 图可以被拓扑排序。
对于零出度算法：
如果有时候，我们只需要知道某个 DAG 图是否可以拓扑排序，而不需要真正得到拓扑排序后的结果，那么可以不需要结果栈，只需要判断整个深度优先搜索过程，没有发生 “搜索中” 节点的相邻节点（不包含来路的节点）也是 “搜索中” 就行。

图的概述 ​

图的定义 ​

相邻 ​

简单图 ​

路径和环路 ​

度数 ​

子图 ​

连通 ​

无向图 ​

有向图 ​

割 ​

稀疏图/稠密图 ​

补图 ​

反图 ​

特殊的图 ​

同构 ​

无向简单图的二元运算 ​

特殊的点集/边集 ​

支配集 ​

边支配集 ​

独立集 ​

匹配 ​

点覆盖 ​

边覆盖 ​

团 ​

图的存储 ​

直接存边 ​

方法 ​

代码实现 ​

复杂度 ​

应用 ​

关联矩阵 ​

邻接矩阵 ​

方法 ​

代码实现 ​

复杂度 ​

应用 ​

点操作和边操作 ​

点操作 ​

边操作 ​

邻接表 ​

方法 ​

代码 ​

基于链表的邻接表 ​

复杂度 ​

应用 ​

链式前向星 ​

引入 ​

语义约定 ​

时间复杂度总结 ​

参考资料 ​

平面图 ​

定义 ​

性质 ​

Jordan曲线定理 ​

平面图的次数公式 ​

欧拉定理 ​

例子 ​

K5的非平面性 ​

K3,3的非平面性 ​

参考资料 ​

深度优先搜索 ​

引入 ​

特征 ​

时间复杂度 ​

实现 ​

栈实现 ​

递归实现 ​

邻接表 ​

链式前向星 ​

DFS 序列 ​

括号序列 ​

一般图上 DFS ​

广度优先搜索 ​

引入 ​

代码实现 ​

open-closed 表 ​

在树/图上 BFS ​

BFS 序列 ​

一般图上 BFS ​

图的概述

图的定义

相邻

简单图

路径和环路

度数

子图

连通

无向图

有向图

割

稀疏图/稠密图

补图

反图

特殊的图

同构

无向简单图的二元运算

特殊的点集/边集

支配集

边支配集

独立集

匹配

点覆盖

边覆盖

团

图的存储

直接存边

方法

代码实现

复杂度

应用

关联矩阵

邻接矩阵

方法

代码实现

复杂度

应用

点操作和边操作

点操作

边操作

邻接表

方法

代码

基于链表的邻接表

复杂度

应用

链式前向星

引入

语义约定

时间复杂度总结

参考资料

平面图

定义

性质

Jordan曲线定理

平面图的次数公式

欧拉定理

例子

K5的非平面性

K3,3的非平面性

参考资料

深度优先搜索

引入

特征

时间复杂度

实现

栈实现

递归实现

邻接表

链式前向星

DFS 序列

括号序列

一般图上 DFS

广度优先搜索

引入

代码实现

open-closed 表

在树/图上 BFS

BFS 序列

一般图上 BFS