堆（Heap）

定义

1. 堆通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质：

   1. （堆序性）堆中某个节点的值总是不大于或不小于其父节点的值；

   2. （结构性）堆总是一棵完全二叉树（除最后一层外，其他层节点都有两个子节点，并且最后一层节点都左排列）。

将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。常见的堆有二叉堆（实现大根堆、小根堆的主要方法）、斐波那契堆等。

//小根堆
								2(Root)
        +-----------------------+------------------+
		4										   5
    +---+-------------+                   +--------+
  	9           	  10				 11(Last Node)

Theorem: A heap storing n keys has height $O(\log n)$

Proof: (Using properties of Complete Binary Tree)

Let h be the height of a heap storing n keys

Since there are $2^i$keys at depth $i=0,\dots ,h-1$,

and at least one key at depth $h$, we have $n\ge 1+2+4+\dots +2^{h-1}-1$

Hence, $n\ge 2^h$, i.e., $h\le \log n$

用堆实现优先队列

若insert()和delMin()操作的时间复杂度线性正比于堆的高度，则它们都可以在$O(\log n)$时间内完成这两种操作。堆在物理上可以借助向量实现。内部节点的最大Rank：$\lfloor {\displaystyle \frac{n-2}{2}}\rfloor$

#define Parent(i) (((i) - 1) >> 1)
#define LChild(i) (1 + ((i) << 1))
#define RChild(i) ((1 + (i)) << 1)

即：对于一个Rank为i的节点node:

• 其左孩子的Rank为2i+1

• 其右孩子的Rank为2i+2

• 其父节点的Rank为(i-1)/2。

利用堆结构来表示的优先队列，包括了如下的要素：

1. 堆H。即一棵完全二叉树，其中各节点存有条目并根据其关键码满足堆序性。可以通过向量实现H。为了叙述方便，以下用k(v)来表示节点v（所存放的）条目的关键字。
2. 比较器C。

在查询规模时，实际上是在查询H的规模。因为二叉树由向量实现，所以isEmpty()和getSize()均可以在$O(1)$时间内完成。若要获取堆顶，只需要取出向量中Rank==1的元素即可。

public class ComplBinTree_Vector extends BinTree_LinkedList implements ComplBinTree {
	private Vector T;//向量
	
//构造方法：默认的空树
	public ComplBinTree_Vector()
	{ T = new Vector_ExtArray();	root = null; }

//构造方法：按照给定的节点序列，批量式建立完全二叉树
	public ComplBinTree_Vector(Sequence s)
	{ this();	if (null !=s) while (!s.isEmpty()) addLast(s.removeFirst()); }
}

插入与上滤（insert(key, e)操作的实现）(UpHeap)

1. 通过完全二叉树的addLast()方法，将条目v=(key,e)作为末尾节点插入到堆中。此时，由于至少插入到了最后一层，堆的结构性未被破坏，堆仍是一棵完全二叉树。

2. 插入后，除非H原先为空，否则v必有父亲。对于v和器父亲u的关键码大小有两种可能（以小根堆举例）：key(v) ≥ key(u)或者key(v)<key(u)。若为后者，则堆的堆序性不再满足，必须进行父亲和孩子的交换。注意：此交换可能会进行多次，直到整个堆的堆序性得到满足。

3. 上滤(Percolating Up)：指新插入节点通过与父亲交换不断向上移动的这一过程。如果利用向量完成二叉树，每一次交换只需要$O(1)$时间，则insert()的操作的时间复杂度为$O(\log n)$

4. 代码实现：

   //上滤算法
   	protected void percolateUp(BinTreePosition v) {
   		BinTreePosition root = H.getRoot();//记录根节点
   		while (v != H.getRoot()) {//不断地
   			BinTreePosition p = v.getParent();//取当前节点的父亲
   			if (0 >= comp.compare(key(p), key(v)))	break;//除非父亲比孩子小
   			swapParentChild(p, v);//否则，交换父子次序
   			v = p;//继续考察新的父节点（即原先的孩子）
   		}
   	}

   English Version:

   After the insertion of a new key k at the node z, the heap-order property may be violated

   Algorithm upheap restores the heap order property by swapping k along an upward path from the insertion node

   Up-heap terminates when the key k reaches the root or a node whose parent has a key smaller than or equal to k

   Since a heap has height $O(\log n)$, up-heap runs in $O(\log n)$time

删除与下滤（delMin()操作的实现）(DownHeap)

1. 若将堆顶删除之后，堆的结构性不再满足。为了恢复其结构性，简便做法是最末尾的节点v移动至堆顶位置。

2. 若堆中剩余至少两个节点，则移动至堆顶的v必然有后代。此时，由于v是从堆底移动上来的，堆的堆序性无法得到满足。这里，对称地运用上滤操作：如果v与孩子之间违背堆序性，我们在v的两个孩子中挑选出更小者（记作u，实际上u也是v及其两个孩子中的最小者），并将v与u交换。经过这样的一次交换，v将下降一层；而更重要的是，v及其（原先的）两个孩子之间的堆序性随即得到恢复。如此重复，直到整个堆的堆序性得到恢复。

3. 下滤(Percolating Down)：指堆顶节点通过与孩子交换不断向下移动的这一过程。如果利用向量完成二叉树，每一次交换只需要$O(1)$时间，则delMin()的操作的时间复杂度为$O(\log n)$

4. 代码实现：

   //下滤算法
   	protected void percolateDown(BinTreePosition v) {
   		while (v.hasLChild()) {//直到v成为叶子
   			BinTreePosition smallerChild = v.getLChild();//首先假设左孩子的（关键码）更小
   			if (v.hasRChild() && 0 < comp.compare(key(v.getLChild()), key(v.getRChild())))
   				smallerChild = v.getRChild();//若右孩子存在且更小，则将右孩子作为进一步比较的对象
   			if (0 <= comp.compare(key(smallerChild), key(v))) break;//若两个孩子都不比v更小，则下滤完成
   			swapParentChild(v, smallerChild);//否则，将其与更小的孩子交换
   			v = smallerChild;//并继续考察这个孩子
   		}
   	}

   English Version:

   After replacing the root key with the key k of the last node w, the heap-order property may be violated

   Algorithm downheap restores the heap order property by swapping k along a downward path from the root

   Down-heap terminates when the key k reaches a leaf or a node whose children have keys larger than or equal to k

   Since a heap has height $O(\log n)$, down-heap runs in $O(\log n)$time

建堆（Heapification）

1. 蛮力算法（自上而下）：反复调用insert()方法建立完全二叉堆。每一次调用insert()方法要$O(\log n)$间，故依次插入所有$n$个节点需要$O(\log n)$间。

$$T(n)=O(\log 1)+O(\log 2)+\dots +O(\log n)=O(\log n!)=O(\log n^n)=O(n\log n)$$

这里，我们甚至可以先利用时间复杂度为$O(n\log n)$的算法(QuickSort, MergeSort)对元素按照关键码进行全排序，再依次插入。所以，用蛮力建立堆并不可取。

1. Robert Floyd算法（自下而上）：将上述蛮力建堆策略的处理方向与次序颠倒过来。首先，将所有节点存储为一棵完全二叉树，从而满足结构性和完整性。为了恢复堆序性，可以自下而上，对各个内部节点实施下滤操作。在所有内部节点都经过下滤之后，二叉树处处都将满足堆序性，亦即成为一个名副其实的堆。

   建堆策略（Heapify Algorithm）：

   1. Starting at index $i=\lfloor {\displaystyle \frac{n}{2}}\rfloor -1$;
   2. Call downheap() until $i=0$, decrementing $i$ at each step.

   结论：任意给定分别以r0、r1为根节点的堆H0、H1以及节点p。为了得到对应于$H_0\cup H_1\cup p$的一个堆，只需将r0和r1当作p的孩子，然后对p进行下滤。

   算法：Heapificate(N[], n) 
   输入：n个堆节点组成的序列N[] 
   输出：将输入的节点组建为一个堆 
   说明：Robert Floyd算法，O(n)时间 
   { 
       创建容量为n的空堆H; 
       将N[]中的n个节点直接复制到堆中; //结构性自然得到满足 
       自底而上，依次下滤各内部节点; //此后堆序性也必然满足 
       返回H; 
   }

   public PQueue_Heap(Comparator c, Sequence s) {
       comp = c;
       H = new ComplBinTree_Vector(s);
       if (!H.isEmpty()) {
           for (int i = H.getSize()/2-1; i >= 0; i--)//自底而上
           	percolateDown(H.posOfNode(i));//逐节点进行下滤
       }
   }

   该方法的效率分析：首先，在完全二叉树中对高度为h的任意节点进行下滤，最多要进行h次节点交换。若记堆的高度为d，则高度为h的节点不会多于$2^{d-h}$个，因此，若该算法下滤操作的时间为$S(n)$，堆的规模为$n$，则有

$$S(n)\le \sum _{h=0}^d(h\cdot 2^{d-h})=2^{d+1}-d-2<2^{d+1}$$

考虑到完全二叉树的上面$d$层（深度为0至d-1）的所有节点构成一棵满树，则有

$$n\ge 2^d-1$$

于是，有

$$S(n)<2(n+1)=O(n)$$

故所有下滤操作总共只需线性的时间。考虑到将n个节点组织为一棵完全二叉树也可以在线性时间内完成，有

只需$O(n)$时间，即可将$n$个条目组织为一个二叉堆结构。

1. 在一个大顶堆中，最小元素通常位于堆的底部，因此直接找到并删除最小元素的操作复杂度是$O(n)$，而不是$O(\log n)$这是因为我们需要遍历整个堆来找到最小元素。在删除元素后，我们还需要重新调整堆，这又是一个$O(\log n)$操作。所以，总的时间复杂度是$O(n)$。

   如果你需要在$O(\log n)$时间复杂度内执行获取和删除最小元素的操作，一种常见的做法是使用一个额外的小顶堆来存储所有的元素。这样，大顶堆可以用来快速获取和删除最大元素，而小顶堆可以用来快速获取和删除最小元素。这种数据结构通常被称为“双堆”或“双端优先队列”。

   请注意，这种方法的缺点是插入操作的时间复杂度会变为$O(\log n)$因为每次插入元素时，都需要在两个堆中进行操作。同时，这也会增加存储空间的需求，因为需要存储两个堆。

斐波那契堆的实现原理

1. 斐波那契堆是一种非常高效的优先队列数据结构，它的主要优点是许多操作的平摊时间复杂度可以达到$O(1)$。
2. 斐波那契堆的实现比二叉堆复杂得多，主要是因为它使用了一种称为"级联剪切"的技术来保持其高效性。斐波那契堆的基本结构是一组最小堆有序树的集合，这些树都满足斐波那契堆的性质。在斐波那契堆中，每个节点包含一个关键字（key）和两个指针，一个指向它的子节点，一个指向它的兄弟节点。每个节点还有一个布尔值"标记"（mark），用于在节点的子节点被删除时进行标记。
3. 斐波那契堆的主要操作包括插入、查找最小值、删除最小值和合并两个堆。以下是这些操作的基本原理：
   1. 插入：新节点被添加到根列表中，时间复杂度为$O(1)$。
   2. 查找最小值：由于所有的根节点都在根列表中，所以查找最小值只需要遍历根列表，时间复杂度为$O(1)$。
   3. 删除最小值：首先找到最小值节点，然后将其所有子节点添加到根列表中，然后删除最小值节点。最后，为了保持斐波那契堆的性质，需要进行一次"合并"操作，将度数相同的树合并在一起。这个操作的平摊时间复杂度为$O(\log n)$。
   4. 合并：将两个斐波那契堆的根列表合并在一起，然后进行一次"合并"操作，将度数相同的树合并在一起。这个操作的时间复杂度为$O(1)$。
4. 斐波那契堆的关键操作是**"级联剪切"，当一个节点失去一个子节点时，如果该节点未被标记**，则将其标记；如果已被标记，则将其从其父节点中剪切出来，添加到根列表中，并递归地对其父节点进行同样的操作。这个操作保证了斐波那契堆的高效性。

堆排序(HeapSort)

什么是堆排序

1. 堆排序是由1991年的计算机先驱奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德(Robert W. Floyd)和威廉姆斯(J. Williams)在1964年共同发明了的一种排序算法。

2. 该排序算法分为前后两个阶段。第一阶段，是将待排序的n个元素组织为一个优先队列Q，然后，不断地将优先队列中最小的元素摘出，使得它们依次构成一个有序的序列。在堆排序中，第一阶段的建堆操作仅需要花费线性时间$O(n)$，第二阶段反复调用delMin()方法，不断地取出Q中的最小元素，这样，n次调用需要花费$O(n\log n)$时间，总的时间复杂度为$O(n\log n)$。

定理 基于比较操作的排序算法具有$\mathrm{\Omega }(n\log n)$的时间复杂度下界。证明详见算法设计与分析的相关章节。

就地堆排序(In-place Heapsort)

1. 就地算法(In-place Algorithm)：除输入本身外只使用常数辅助空间的算法，称作就地算法。

2. 许多情况下，等待排序的$n$个元素都以一个长度为$n$的数组S[]形式给出。为此，除了输入数组以外，我们还需要为堆结构消耗$O(n)$的辅助空间。而实际上，这个空间的规模完全可以降低到$O(1)$。

3. 算法思路：算法的总体思路和策略与选择排序算法基本相同：将所有词条分成未排序和已排序两类，不断从前一类中取出最大者，顺序加至后一类中。算法启动之初，所有词条均属于前一类；此后，后一类不断增长；当所有词条都已转入后一类时，即完成排序。

4. 具体的实现：

   1. 将其划分为前缀H和与之互补的后缀S，分别对应于上述未排序和已排序部分。与常规选择排序算法一样，在算法启动之初H覆盖所有词条，而S为空。注意：这里，若从小到大进行排序，则H应为大根堆。

   2. 不同之处：整个排序过程中，不论H有多少词条，其始终都组织成一个堆。另外，整个算法过程始终满足如下不变性：H中的最大词条不会大于S中的最小词条——除非二者之一为空，比如算法的初始和终止时刻。

   3. 首先取出H中的堆顶M，与末单元词条X交换。M既是当前堆中的最大者，同时根据不变性，也不大于S中的任何词条，故如此交换之后M必处于正确的排序位置。此时，可以等效地认为S扩大了一个单元，而H相应地缩小了一个单元。这里，H和S仍然满足不变性。

   4. 有很大的可能，X不能称为堆顶，否则会破坏堆的堆序性。此时，可以对X进行下滤，就能使得H的堆序性重新恢复。

      对于大根堆的下滤操作，交换时应选择其两个孩子的最大者。

   5. 重复第3，4步，直到整个排序完成。

5. 复杂度：在每一步迭代中，交换M和X只需常数时间，对X的下滤调整不超过$O(\log n)$时间。因此，全部$n$步迭代累计耗时不超过$O(n\log n)$。即便使用蛮力算法而不是Floyd算法来完成H的初始化， 整个算法的运行时间也不超过$O(n\log n)$。

优先队列

1. 一种特殊的队列。在优先队列中，元素被赋予优先级，当访问队列元素时，具有最高优先级的元素最先删除。

   1. 优先队列与普通队列最大的不同点在于出队顺序。
   2. 普通队列的出队顺序跟入队顺序相关，符合「先进先出（First in, First out）」的规则。
   3. 优先队列的出队顺序跟入队顺序无关，优先队列是按照元素的优先级来决定出队顺序的。优先级高的元素优先出队，优先级低的元素后出队。优先队列符合 「最高级先出（First in, Largest out）」 的规则。

2. 优先队列的应用场景非常多，比如：

   • 数据压缩：赫夫曼编码算法；
   • 最短路径算法：Dijkstra 算法；
   • 最小生成树算法：Prim 算法；
   • 任务调度器：根据优先级执行系统任务；
   • 事件驱动仿真：顾客排队算法；
   • 排序问题：查找第 k 个最小元素。

3. 关键码、比较器与偏序关系

   1. 词条(Entry)：仿照词典结构，我们也将优先级队列中的数据项称作词条。

   2. 关键码(Key)：与特定优先级相对应的数据属性，也称作关键码。注意：关键码之间必须可以比较大小。作为优先队列的一个基本要求，在关键码之间必须能够定义某种全序关系(Total Order Relation)。该关系必须满足下述三条性质：

      自反性：对于任意关键码k，都有k ≤ k /可比较性：对于任意的关键码x,y均有x ≤ y或y ≤ x

      反对称性：若k1 ≤ k2且k2 ≤ k1，则k1 = k2

      传递性：若k1 ≤ k2且k2 ≤ k3，则k1 ≤ k3

4. Entry接口：

   public interface Entry<K,V>{
   	K getKey();
       void setKey(K key);
   	V gatValue();
       void setValue(V value);
   }

   1. In our lecture, we assume that an element's key remains fixed once it has been added to a priority queue.
   2. Fixed keys does not mean fixed order.
   3. The priority (order) of a job is not fixed, may change when the whole set of jobs change in the queue. This is meaning that jobs need to be reordered.

5. 比较器：

   1. 与C++不同，Java不支持对比较操作符> < ==的重载。我们需要基于某种Comparable接口实现一个关键码类，并将所有通常的比较方法封装起来，以支持关键码之间的比较。但是，如果按照关键码本身的类型来决定关键码的比较方式，那么在很多情况下，这并不能最终决定关键码的具体比较方式。如3和12，按照整型和字符串类型（字典序）比较，会得到不同的结果。

   2. 不如基于Comparator接口专门实现一个独立于关键码之外的比较器类，由它来确定具体的比较规则。在创建每个优先队列时，只要指定这样一个比较器对象，即可按照该比较器确定的规则，在此后进行关键码的比较。这一策略的另一优点在于，一旦不想继续使用原先的比较器对象，可以随时用另一个比较器对象将其替换掉，而不用重写优先队列本身。

   3. 代码实现：

      public interface Comparator{
      	public int compare(Object a, Object b);
      }

      每一次进行比较时，基于该接口实现需要的比较类和方法。

      默认情况下的比较器：

      public class ComparatorDefault implements Comparator { //实现该类
          public ComparatorDefault() {} 
          public int compare(Object a, Object b) throws ClassCastException { 
          	return ((Comparable) a).compareTo(b); //实现该方法
          } 
      }

6. 优先队列的ADT及代码实现：

   1. 操作接口：

   操作接口	功能描述
   size()	报告优先级队列的规模，即其中词条的总数
   insert()	将指定词条插入优先级队列
   getMax()	返回优先级最大的词条（若优先级队列非空）
   delMax()	删除优先级最大的词条（若优先级队列非空）

   2. Java接口：

      public interface PQueue { 
          //统计优先队列的规模 
          public int getSize(); 
          //判断优先队列是否为空 
          public boolean isEmpty(); 
          //若Q非空，则返回其中的最小条目（并不删除）;否则，报错 
          public Entry getMin() throws ExceptionPQueueEmpty; 
          //将对象obj与关键码k合成一个条目，将其插入Q中，并返回该条目 
          public Entry insert(Object key, Object obj) throws ExceptionKeyInvalid; 
          //若Q非空，则从其中摘除关键码最小的条目，并返回该条目；否则，报错 
          public Entry delMin() throws ExceptionPQueueEmpty; 
      }

   3. 基于优先队列的排序器：

      public class Sorter_PQueue implements Sorter {
          private Comparator C;
          public Sorter_PQueue()
         		{ this(new ComparatorDefault()); }
          public Sorter_PQueue(Comparator comp)
         		{ C = comp; }
          public void sort(Sequence S) {
              Sequence T = new Sequence_DLNode();//为批处理建立优先队列而准备的序列
              while (!S.isEmpty()) {//构建序列T
                  Object e = S.removeFirst();//逐一取出S中各元素
                  T.insertLast(new EntryDefault(e, e));//用节点元素本身作为关键码
              }
              PQueue pq = new PQueue_Heap(C, T);
              while(!pq.isEmpty()) {//从优先队列中不断地
                  S.insertLast(pq.delMin().getValue());//取出最小元素，插至序列末尾
                  System.out.println("\t:\t" + S.last().getElem());
              }
          }
      }//每一次都要排序

7. 用向量和列表实现优先队列：

   1. 使用向量实现优先队列：（不推荐）

   2. 使用无序列表实现优先队列：

      思想：为了插入一个被赋予关键码key的对象obj，我们首先创建一个条目对象entry = (key, obj)，然后调用insertLast(entry)方法将其接至列表尾部。时间复杂度$O(1)$。这样构造的列表是无序的，所以无论使用getMin()还是delMin()方法，都需要对整个列表进行一次扫描。则要花费$O(n)$时间才能找到最小条目（最重要元素）。

   3. 使用有序列表实现优先队列：

      思想：欲提高delMin()方法的效率，可以要求所有条目按非升次序排列。这样仅需调用removeLast()就可以在$O(1)$时间内去掉末尾的最小条目（最重要元素）。但是，为了维护列表的有序性，在插入时，必须找正确的插入位置，即遍历列表。故在此方法中，insert()方法的时间复杂度为$O(n)$。

   4. 时间复杂度：

      Method	Unsorted List	Sorted List
      min()	${\color{Green} O(n)} $	$O(1)$
      insert()	$O(1)$	${\color{Green} O(n)} $
      removeMin()	${\color{Green} O(n)} $	$O(1)$
      size()	$O(1)$	$O(1)$
      isEmpty()	$O(1)$	$O(1)$

      Consider these $O(n)$ algorithms. Can we do better? That means, we traverse this Priority Queue when executing min(), insert() and removeMin() , which are $O(n)$ methods. If we can impel these method in $O(\log n)$， that would be better.

8. 有关排序算法——选择排序和插入排序

   1. 选择排序：如果采用无序列表来实现优先队列，则PQSort的前一步中的n次insert()操作总共只需要$O(n)$时间。然而，随后一步的效率却太低了——为了执行每一次delMin()操作，需要耗费的时间都将正比于优先队列当前的规模，因此第二阶段总共需要耗费$O(n^2)$的时间。
   2. 插入排序：采用有序列表来实现优先队列，则每次delMin()操作都可以在常数时间内完成，故 PQSort算法后一阶段总的时间复杂度可以降至$O(n)$。然而这并非没有代价。为了维护列表的有序性， 前一阶段中的每一次insert()操作，都需要对当前的列表进行扫描，以确定新条目的插入位置。在最坏的情况下，为此需要花费的时间将正比于优先队列当前的规模。因此，前一阶段的总体时间复杂度为$O(n^2)$。
   3. 效率比较：选择排序的时间为$\mathrm{\Theta }(n^2)$，插入排序最好情况为$O(n)$，最坏情况为$O(n^2)$。
   4. 实现优先队列最高效的结构，就是借助**堆(Heap)**结构。

编码树、Huffman树——二叉树的应用实例

简介与二进制编码

1. 通讯理论中的一个基本问题是，如何在尽可能低的成本下，以尽可能高的速度，尽可能忠实地实现信息在空间和时间上的复制与转移。在现代通讯技术中，无论采用电、磁、光或其它任何形式，在信道上传递的信息大多以二进制比特的形式表示和存在，而每一个具体的编码方案都对应于一棵二叉编码树。

2. 通讯系统可以帮助人们将一段信息从发送端传送给接收端。最常见的信息形式是字符串，即由来自某一有限字符集$\mathrm{\Sigma }$的若干个字符组成的一个序列$M=(x_1,\dots ,x_n),x_i\in \mathrm{\Sigma },1\le i\le n$。在将$M$加载至信道上并发送之前，首先需要对$M$进行编码（Encoding）。通常采用的都是二进制编码⎯⎯对于$\mathrm{\Sigma }$​中的每个字符c，分别指定一个二进制串e(c)，这可以描述为如下单射函数：

$$e():\mathrm{\Sigma }\mapsto \{0,1{\}}^{\ast }$$

3. 解码（Decoding）：接收端在收到该二进制中，可以利用对应的逆函数进行解码，这样能看到对应的函数内容。

$$e^{-1}():\{0,1{\}}^{\ast }\mapsto \mathrm{\Sigma }$$

4. 实例：以英文字符集$\mathrm{\Sigma }=\{A,B,C,\dots ,Z\}$为例，若要传送字符串MAIN，则一种可行的编码方式为

   e('N')="00", e('A')="010", e('I')="011", e('M')="1".

   "1 010 011 00"-> "MAIN"

                              Root
        +-----------------------+------------------+
   		0										   M(1)
    +---+-------------+                   
   	N(00)             1
     			  +---+----+
     		 (010)A        I(011)

5. 二进制编码：对于任意给定的文本， 通过查阅编码表逐一将其中的字符转译为二进 制编码，这些编码依次串接起来即得到了全文的编码。

6. 二进制解码：由编码器生成的二进制流经信道送达之后，接收方可以按照事先约定的编码表（表5.1）， 依次扫描各比特位，并经匹配逐一转译出各字符，从而最终恢复出原始的文本。

7. 解码歧义：编码方案确定之后，尽管编码结果必然确定，但解码过程和结果却不见得唯一。如，把M编码为11，把S编码为111，则111111既可以表示MMM，又可以表示SS。所以，为了避免这种情况，我们需要一种前缀无歧义编码（Prefix-Free Code, PFC）。

PFC编码

1. 此类编码算法，可以明确地将二进制编码串，分割为一系列与各原始字符对应的片段，从而实现无歧义的解码。得益于这一特点，此类算法在整个解码过程中，对信息比特流的扫描不必回溯。
2. PFC编码可以使用二叉编码树来实现。任一编码方案都可描述为一棵二叉树：从根节点出发，其中，每一“父亲-左孩子”关系对应于一个二进制位'0'，每一“父亲-右孩子”关系对应于一个二进制位'1'。于是，若令每个字符分别对应于一匹叶子，则从根节点通往每匹叶子的路径，就对应于相应字符的二进制编码。因此， 这样的一棵树也称作二叉编码树。
3. 根通路串（Root Path String）：由从根节点到每个节点的唯一通路，可以为各节点v赋予一个互异的二 进制串，称作根通路串，记作rps(v)。|rps(v)|=depth(v)就是v的深度。若将$\mathrm{\Sigma }$中的字符分别映射至二叉树的节点，则字符x的二进制编码串即可取rps(v(x))，简记为rps(x)。
4. PFC编码树和编码方案：只要所有字符都对应于叶节点，歧义现象即自然消除——这也是实现PFC编码的简明策略。
5. 基于PFC编码树的解码：从头开始扫描接收到的二进制信息流，从根节点开始，根据各比特位不断进入下一层节点；到达叶子节点后，输出其对应的字符，然后重新回到根节点，并继续扫描二进制流。实际上，这一个过程可以在接收过程中实时进行，而不必等到所有的比特位都到达之后再开始解码。（在线算法）

最优编码树

1. 通讯效率的问题：我们希望使用尽可能少的比特位来表示字符串。

2. 平均编码长度：若将字符c在二叉编码树中对应的叶子的深度记为depth(c)，则有

   每一个字符$c\in \mathrm{\Sigma }$的编码长度为$|e(c)|=\text{depth}(c)$。（观察即可得出规律）

3. 定义1：

   对于任一字符集$\mathrm{\Sigma }$的任一编码方式$e()$，$\mathrm{\Sigma }$中各字符的编码长度总和$\mathrm{\Sigma }|e(c)|$称作$e()$（或其 $c\in \mathrm{\Sigma }$对应的二叉编码树）的编码总长度；单个字符的平均编码长度为$\mathrm{\Sigma }|e(c)|/|\mathrm{\Sigma }|$。

   平均编码长度是反映编码效率的一项重要指标，我们希望这一指标尽可能地小。

4. 定义2（最优编码树）：

   对于任一字符集$\mathrm{\Sigma }$，若在所有的编码方式中，某一编码方式$e()$使得平均编码长度最短，则称$e()$为$\mathrm{\Sigma }$的一种最优编码，与之对应的编码树称作$\mathrm{\Sigma }$的一棵最优编码树。

   对于同一字符集$\mathrm{\Sigma }$，所有深度不超过$|\mathrm{\Sigma }|$的编码树仅有有限课，故长度最小者必然存在，但可能并不唯一。

5. 最优编码树的性质：在最优二叉编码树中，

   1. （双子性）每个内部节点的度数均为2；

      证明：（反证法）假设在某棵最优二叉编码树T中存在一个度数为1的内部节点p，不妨设p唯一的孩子为节点c。于是，只要将节点p删除，并代之以子树c，则可以得到原字符集的另一棵编码树T'。不难看出，除了子树c中每匹叶子的编码长度均减少1之外，其余叶子的编码长度不变，因此与T相比，T'的平均编码长度必然更短——这与T的最优性矛盾。（换句话说，度数为1的节点相当于多给它的子树套了一层，完全没有用处）

   2. （平衡性）各叶子之间的深度差不超过1。

      证明：（反证法）假设某棵最优二叉编码树T中存在深度相差超过1的两匹叶子x和y。不妨设x更深，并令p为x的父亲。于是根据双子性，作为内部节点的p必然还有另一个孩子q。注意，子树q中至少含有一匹叶子。

      现在，将叶子y与子树p交换，得到一棵新的树T'。易见，T'依然是原字符集的一棵二叉编码树。更重要的是，除了x、y以及子树q中的叶子外，其余叶子的深度均保持不变。**经过这一交换操作之后，x的深度减少1，y的深度增加1，而q中各叶子的深度都将减少1。**因此，与T相比，T'的平均编码长度必然更短——这与T的最优性矛盾。 （换句话说，让一个变深，让一群变浅）

   3. 推论：（用来构造最优编码树）

      基于由$2|\mathrm{\Sigma }|-1$个节点构成的完全二叉树T，将$\mathrm{\Sigma }$中的字符任意分配给$T$的$|\mathrm{\Sigma }|$匹叶子，即可得到$\mathrm{\Sigma }$的一棵最优编码树。

完全二叉编码树

1. 一种最直接的思想是，构造完全二叉编码树来实现最优编码。这种方法，使得所有字母的编码长度都一样，看似是比较完善的一种方案。但是，这种方案没有考虑到字符出现的频率。

2. 例子：英文字母的出现概率：某些字母，如e,t等，出现的频率是某些字母，如z,j等频率的数百倍。这样，我们应该从另一个角度衡量每个字符的编码长度。

3. 平均带权编码长度：若假设字符c出现的概率为$p(c)\ge 0,\sum _{c\in \mathrm{\Sigma }}p(c)=1$，将其在二叉编码树中对应的叶子的深度记作depth(c)，则（定义）：

   1. 每个字符 $c\in \mathrm{\Sigma }$ 的带权编码长度为 $|e(c)|=\text{depth}(c) \times p(c) $。

   2. 对于任一字符集 $\mathrm{\Sigma }$ 的任一编码方式$e()$, $\mathrm{\Sigma }$中各字符的平均带权编码长度总和 $\sum _{c\in \mathrm{\Sigma }}|e(c)|$ 称作 $e()$ （或其对应的二叉编码树）的平均带权编码长度。

   不难理解，在考虑字符出现频率时，如上定义的平均带权编码长度就是反映编码效率的一项重要指标，我们同样也希望这一指标尽可能地小。

   如：对于e('M')="00", e('A')="001", e('I')="01", e('N')="1"来说，
   编码"00000100000110 1"="MAMANI",平均带权编码长度=15/6=2.5。
   |e('M')|=3{深度}*(2/6){频率}=1{带权编码长度}
   |e('M')|+|e('A')|+|e('I')|+|e('N')|=2.5{平均带权编码长度}

4. 完全二叉编码树 ≠ 平均带权编码最短

   还是从上面的例子分析，若我们使用完全二叉编码树，对于拥有4个元素的字符集，不论字符出现频率的大小，其对应的平均带权编码长度都是2。但是，当某一个字符数量较多的时候，我们可以调整编码树，不使用完全二叉编码树，让字符频率高的享有较短编码，这样可以进一步降低平均带权编码长度。

最优带权编码树

1. 定义：对于任一字符集$\mathrm{\Sigma }$，在字符出现频率分布为$p()$时，若某一编码方式$e()$使得平均带权编码长度达到最短，则称$e()$为（按照$p()$分布的）$\mathrm{\Sigma }$ 的一种最优带权编码，其对应的编码树称作（按照$p()$分布的）$\mathrm{\Sigma }$的一棵最优带权编码树。其必然存在，而且通常也不唯一。

2. 性质：

   1. （双子性）在最优带权编码树中，内部节点的度数均为2。证明方法如上。

   2. （层次性）对于字符出现概率为$p()$的任一字符集$\mathrm{\Sigma }$，若字符x和y在所有字符中的出现概率最低，则必然存在某棵最优带权编码树，使得x和y在其中同处于最底层，而且互为兄弟。

   证明：

   任取一棵最优带权编码树T。

   根据最优带权编码树的双子性，在T的最低层节点中，必然可以找到一对兄弟a和b。现在，我们交换节点a和x（如果它们不是同一节点的话），并且交换节点b和y（如果它们不是同一节点的话），从而得到同一字符集的另一棵编码树T'。交换前，a,b是兄弟，而x和y关系未知。交换后，x和y为兄弟。

   另外，根据字符x和y的权重最小性，经过这样的交换，T'对应的平均带权编码长度 绝不会增加。于是根据T的最优性，T'必然也是一棵最优编码树。

Huffman编码树

1. 定义：Huffman编码树是一棵满二叉树，其中的每一个叶子节点都对应一个在给定的字符集中出现的字符，并且是一棵满足层次性的最优带权编码树。

2. Huffman编码树的构造算法——推论奠基

   设在字符的某一出现概率分布$p()$下，字符集$\mathrm{\Sigma }$中出现概率最低的两个字符为x和y。现考察另一字符集${\mathrm{\Sigma }}^{\prime }=(\mathrm{\Sigma }\mathrm{\setminus }\{x,y\})\cup \{z\}$（即剔除了x和y，增加了z），并将新增字符$z$的出现概率设为$p(z)=p(x)+p(y)$，其余字符的出现概率保持不变。若取T'为$\mathrm{\Sigma }$'对应的一棵Huffman编码树，则根据Huffman编码树的层次性，不难得出如下推论：

   将$T^{\prime }$中与字符$z$对应的叶子替换为一个内部节点，并在其下设置分别对应于$x$和$y$的两匹叶子，则所得到就是$\mathrm{\Sigma }$的一棵Huffman编码树。

   证明：（正向思维） 首先，$T^{\prime }$满足Huffman编码树的层次性，并且$z$已经是一匹叶子。现在在$z$下面增加$x$和$y$两匹叶子，则必然满足最优带权编码树的双子性和层次性两个性质，即为$\mathrm{\Sigma }$的一棵Huffman编码树。

3. Huffman编码树的构造过程——具体实现

   1. 初始化：由给定的n个权值构造 棵只有一个根节点的二叉树，得到一个二叉树集合（森林）F。
   2. 选取与合并：从二叉树集合F中选取根节点权值 最小的两棵 二叉树分别作为左右子树构造一棵新的二叉树，这棵新二叉树的根节点的权值为其左、右子树根结点的权值和。
   3. 删除与加入：从F中删除作为左、右子树的两棵二叉树，并将新建立的二叉树加入到F中。
   4. 重复 2、3 步，当集合中只剩下一棵二叉树时，这棵二叉树就是霍夫曼树。

4. Huffman编码树的构造过程——例子

   

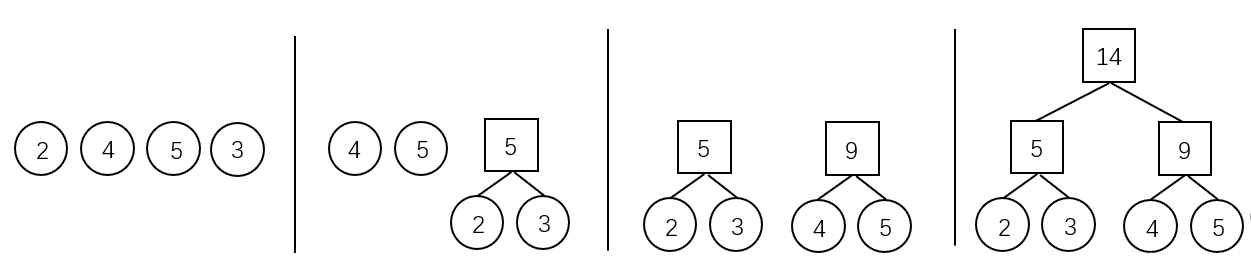
5. 树的带权路径长度

   设二叉树具有n个带权叶结点，从根结点到各叶结点的路径长度与相应叶节点权值的乘积之和称为 树的带权路径长度(Weighted Path Length of Tree，WPL)。设$w_i$为二叉树第$i$个叶结点的权值，$l_i$为从根结点到第$i$个叶结点的路径长度，则 WPL 计算公式如下：

$$WPL=\sum _{i=1}^n{w}_i{l}_i$$

关于Huffman树的构造算法，还需要考虑一些退化情况。比如，有些字符的出现频率可能相等，或者虽然最初的字符权重互异，但经过若干次合并之后，森林F也可能会出现权重相等的子树。于是，在挑选权重最小的两棵子树时，将有可能出现歧义。这里，随便选中一个权重最小的子树即可，因为最后计算出来的$WPL$相等。

6. 霍夫曼编码：构建好Huffman树后，按照一定的次序（如左边为0，右边为1），从根节点向叶子节点延伸编码，最后字符所对应的一个二进制串即为该字符的Huffman编码。

7. 基于优先队列的Huffman树构造算法

   1. 若使用普通的数据结构，构建森林$O(n)$，挑选出权重最小的两棵树$O(n)$，合二为一$O(1)$，每一次迭代后，森林的规模会减一，一共要经过n-1次迭代后，森林中才会剩下一棵树。所以，总的时间复杂度为$O(n^2)$。
   2. 使用优先队列方法：始终将森林中的所有树（根）组织为一个优先队列，比如基于二叉堆实现的优先队列。这样，只要连续地调用delMin()方法两次，就可以找出当前权重最小的两棵树。在将这两棵树合并为一棵新树之后，可以调用insert()方法将其重新插入优先队列。这一过程将反复进行，每迭代一次，森林的规模就会减小1。因此，经过n-1次迭代，森林中将只包含一棵树，即Huffman编码树。 算法的效率上，两次delMin()、一次insert()操作和一次树的合并，可以在$O(1+3\log n)$时间内完成。所以，总共的时间为$(n-1)\times O(1+3\log n)=O(n\log n)$。