6 支持向量机

支持向量机(Support Vector Machine)是一种经典的二分类模型，基本模型定义为特征空间中最大间隔的线性分类器，其学习的优化目标便是间隔最大化可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。

6.1 间隔与支持向量

间隔

1. 分类学习最基本的想法就是基于训练集D在样本空间中找到一个划分超平面，将不同的类别分隔开。直观上看，如在二分类问题中，我们应该去找位于两类训练样本“正中间”的划分超平面，因为它所产生的分类结果是最为鲁棒的，对未见示例的泛化能力越强。

2. 常用的间隔有两个，一种称之为函数间隔，一种为几何间隔。在支持向量机中使用的是几何间隔。

3. 函数间隔：对于给定的训练数据集$D=\{({\mathbf{x}}_1,y_1),({\mathbf{x}}_2,y_2),\cdots ,({\mathbf{x}}_N,y_N)\}$，定义超平面${\mathbf{w}}^T\mathbf{x}+b=0$关于样本点$({\mathbf{x}}_i,y_i)$的函数间隔为

$${\hat{\gamma }}_i=y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)=y_{i}f(x)$$

定义超平面${\mathbf{w}}^T\mathbf{x}+b=0$关于训练数据集$D$的函数间隔为

$$\hat{\gamma }=min{\hat{\gamma }}_i,(i=1,2,\dots ,n)$$

显然，对于误分类的样本点$({\mathbf{x}}_i,y_i)$，其函数间隔为负。而且，函数间隔的大小依赖于$\mathbf{w}$和$b$的比例尺度，如果$\mathbf{w}$和$b$同时成倍缩放，超平面并没有改变，但函数间隔却成倍增大。因此，函数间隔并不能很好地表示样本点$x_i$距离超平面的远近。因此，我们使用数据点到超平面的真实距离作为间隔的度量。

1. 几何间隔：在样本空间中，划分超平面可以通过线性方程${\mathbf{w}}^T\mathbf{x}+b=0$来进行描述。其中，$w$为法向量，$b$为位移项。样本空间中任意一点$x$到超平面的距离可写为

$$\gamma =\frac{{\mathbf{w}}^T\mathbf{x}+b}{||\mathbf{w}||}$$

此时，为了得到r的绝对值，令r呈上其对应的类别y，即可得到几何间隔的定义：

$${\tilde{\gamma }}_i=y_i\left(\frac{{\mathbf{w}}^T{\mathbf{x}}_i+b}{||\mathbf{w}||}\right)$$

假设平面${\mathbf{w}}^T\mathbf{x}+b=0$能将训练数据集正确分类，即对所有的$({\mathbf{x}}_i,y_i)$，若$y_i=+1$，有$y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)>0$；若$y_i=-1$，有$y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)<0$。

支持向量和最大间隔

• 此时，可以做一次伸缩变换，使得上述等式中的右侧为1。距离超平面最近的这几个训练样本点使得上述等式成立，即

$$y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)=\pm 1$$

这些训练样本点被称为支持向量(Support Vector)。而两个异类支持向量到超平面的距离之和为

$$\gamma =\frac{2}{||\mathbf{w}||}$$

被称为间隔(margin)。

• 支持向量机的学习问题就是求解能够正确划分训练数据集并且使得间隔最大的划分超平面。即

$$\underset{w,b}{max}\frac{2}{||w||}\text{ s.t. }{y}_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1,i=1,2,\dots ,m$$

又因为最大化$||w|{|}^{-1}$，等价于最小化$\frac{1}{2}||w|{|}^2$，因此，上式重写为

$$\underset{w,b}{min}\frac{1}{2}||w|{|}^2\text{ s.t. }{y}_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1,i=1,2,\dots ,m$$

这是一个凸二次规划问题，可以用现成的优化计算包求解。这就是支持向量机的基本型。

6.2 对偶问题

目标：通过求解上文提及的式子来得到搭建个划分超平面所对应的模型

$$f(\mathbf{\text{w}})={\mathbf{\text{w}}}^T\mathbf{\text{x}}+b,$$

其中，$\mathbf{\text{w}},b$是参数。该式子本身是一个凸二次规划问题，可以直接使用现成的工具求解。但是，我们可以通过对偶问题来得到更好的理解。

为什么要将原问题转化为对偶问题？

1. 因为使用对偶问题更容易求解；
2. 因为通过对偶问题求解出现了向量内积的形式，从而能更加自然地引出核函数。

对偶问题和拉格朗日乘子法

1. 对偶问题，顾名思义，可以理解成优化等价的问题，更一般地，是将一个原始目标函数的最小化转化为它的对偶函数最大化的问题。
2. 首先，我们将有约束的原始目标函数转换为无约束的新构造的拉格朗日目标函数：

$$L(\mathbf{w},b,\alpha )=\frac{1}{2}\Vert \mathbf{w}{\Vert }^2-\sum _{i=1}^N{\alpha }_i(y_i(\mathbf{w}\cdot {\mathbf{x}}_{\mathbf{i}}+b)-1)$$

其中，${\alpha }_i\ge 0$是拉格朗日乘子。不难验证，若有一个约束条件不满足，则$maxL=\mathrm{\infty }$；当当所有约束条件都满足时，L的最大值为$\frac{1}{2}\Vert w{\Vert }^2$。因此，原始问题可以转化为求解

$$\underset{\mathbf{w},b}{min}\underset{\alpha }{max}L(\mathbf{w},b,\alpha )$$

的问题。 3. 由于上述问题是先求最大值再求最小值的问题，而现在我们首先就要面对带有需要求解的参数$\mathbf{w}$和$b$的方程，而${\alpha }_i$又是不等式约束，这个求解过程不好做。所以，我们需要使用拉格朗日函数对偶性，将最小和最大的位置交换一下：

$$\underset{\alpha }{max}\underset{\mathbf{w},b}{min}L(\mathbf{w},b,\alpha )$$

这样就将原问题的求最小变成了对偶问题求最大（用对偶这个词还是很形象），接下来便可以先求L对w和b的极小，再求L对α的极大。 4. 首先求$L$对$w,b$的极小：分别求${\displaystyle \frac{\partial L}{\partial w}},{\displaystyle \frac{\partial L}{\partial b}}$，有

$$\begin{array}{rl}{\displaystyle \frac{\partial L}{\partial w}}& =w-\sum _{i=1}^N{\alpha }_i{y}_i{x}_i=0\\ {\displaystyle \frac{\partial L}{\partial b}}& =-\sum _{i=1}^N{\alpha }_i{y}_i=0\end{array}$$

代入$L$中，得到

$$\begin{array}{rl}L(\mathbf{w},b,\alpha )& =\frac{1}{2}\Vert \mathbf{w}{\Vert }^2-\sum _{i=1}^N{\alpha }_i(y_i(\mathbf{w}\cdot {\mathbf{x}}_{\mathbf{i}}+b)-1)\\ & =\frac{1}{2}\Vert \sum _{i=1}^N{\alpha }_i{y}_i{x}_i{\Vert }^2-\sum _{i=1}^N{\alpha }_i(y_i(\sum _{j=1}^N{\alpha }_j{y}_j{x}_j\cdot {\mathbf{x}}_{\mathbf{i}}+b)-1)\\ & =\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j-\sum _{i=1}^N{\alpha }_i(y_i\sum _{j=1}^N{\alpha }_j{y}_j{x}_j\cdot {\mathbf{x}}_{\mathbf{i}}+b)+\sum _{i=1}^N{\alpha }_i\\ & =\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j-\sum _{i=1}^N{\alpha }_i\left(y_i\sum _{j=1}^N{\alpha }_j{y}_j{x}_j\cdot {\mathbf{x}}_{\mathbf{i}}\right)+\sum _{i=1}^N{\alpha }_i\\ & =\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j-\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j+\sum _{i=1}^N{\alpha }_i\\ & =\sum _{i=1}^N{\alpha }_i-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j\end{array}$$

上述求解过程要满足KKT条件（KKT条件是在满足一些有规则的条件下，一个非线性规划问题能有最优化解法的一个必要和充分条件）。

5. 然后求$L$对$\alpha$的极大：通过SMO算法，可以得到$\alpha$的解，从而得到$w,b$的解，进而得到模型。

$$\begin{array}{r}\underset{\alpha }{max}\sum _{i=1}^N{\alpha }_i-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j,\\ s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0,{\alpha }_i\ge 0\end{array}$$

6. 通过求解上述对偶问题，我们可以得到$\alpha$的解，从而得到$w,b$的解，进而得到模型。

$$\begin{array}{rl}w& =\sum _{i=1}^N{\alpha }_i{y}_i{x}_i,\\ b& =-\frac{1}{2}(\underset{i:y_i=-1}{max}\mathbf{w}\cdot {\mathbf{x}}_i+\underset{i:y_i=1}{min}\mathbf{w}\cdot {\mathbf{x}}_i)\end{array}$$

这里实际上只需计算新样本与支持向量的内积，因为对于非支持向量的数据点，其对应的拉格朗日乘子一定为0，根据最优化理论（K-T条件），对于不等式约束$y(w^{\prime }x+b)-1\ge 0$，满足：

$${\partial }_i(y_i(w^T+b)-1)=0$$

这里，至少有一个的拉格朗日乘子大于0。用反证法可以证明。

SMO算法

SMO（Sequential Minimal Optimization）算法是一种求解支持向量机（SVM）优化问题的有效方法。其基本思想是：如果所有的变量的解都满足此最优化问题的KKT条件，那么这个最优化问题的解就得到了。因为KKT条件是该最优化问题的充分必要条件。但是SMO算法并不是一次处理所有变量，而是每次只选择两个变量，固定其他变量，然后针对这两个变量构建一个二次规划问题。这个二次规划问题相对于原始问题要简单很多，可以直接求解，不需要借助于数值优化方法。求解出最优解后，再用这个最优解更新那两个变量，这就完成了一次迭代。SMO算法不断地进行这样的迭代，直到所有变量满足KKT条件为止，这时就找到了原始问题的最优解。

SMO算法的主要步骤如下：

1. 选择一对需要优化的变量，这里有一些启发式的方法可以选择违反KKT条件最严重的变量。
2. 固定其他变量，只考虑这两个变量，将问题简化为二次规划问题求解。
3. 更新这两个变量。
4. 检查是否所有变量都满足KKT条件，如果满足，则结束；否则，返回步骤1。

这种方法的优点是每次只需要处理两个变量的优化问题，大大简化了问题的复杂性。

6.3 核函数

线性不可分问题

• 由于上述的超平面只能解决线性可分的问题，对于线性不可分的问题，例如：异或问题，我们需要使用核函数将其进行推广。

• 一般地，解决线性不可分问题时，常常采用映射的方式，将低维原始空间映射到高维特征空间，使得数据集在高维空间中变得线性可分，从而再使用线性学习器分类。如果原始空间为有限维，即属性数有限，那么总是存在一个高维特征空间使得样本线性可分。

• 若$\varphi (x)$代表一个映射，则在特征空间中的划分函数变为：

$$f\left(\mathbf{x}\right)={\mathbf{w}}^T\varphi (\mathbf{x})+b$$

按照同样的方法，先写出新目标函数的拉格朗日函数，接着写出其对偶问题，求L关于w和b的极大，最后运用SOM求解α。

• 原始问题的对偶问题为：

$$\begin{array}{r}\underset{\alpha }{max}\sum _{i=1}^N{\alpha }_i-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\varphi ({\mathbf{x}}_i{)}^T\varphi ({\mathbf{x}}_j),\\ s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0,{\alpha }_i\ge 0\end{array}$$

• 原分类函数变为：

$$f\left(\mathbf{x}\right)=\sum _{i=1}^N{\alpha }_i{y}_i\varphi ({\mathbf{x}}_i{)}^T\varphi (\mathbf{x})+b$$

核函数

• 求解上述问题的关键在于计算$\varphi ({\mathbf{x}}_i{)}^T\varphi ({\mathbf{x}}_j)$，这个计算量是非常大的，因为它是在高维空间中进行的。为了避免这个问题，我们引入了核函数的概念。我们设想这样一个函数：

$$\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)=⟨({\mathbf{x}}_i),\varphi ({\mathbf{x}}_j)⟩=\varphi ({\mathbf{x}}_i{)}^T\varphi ({\mathbf{x}}_j)$$

其中$\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)$是一个核函数，它的作用是直接计算两个样本在高维空间中的内积，而不需要显式地写出映射函数$\varphi (\mathbf{x})$。这样，我们就可以直接在原始空间中计算内积，而不需要显式地写出映射函数$\varphi (\mathbf{x})$。

• 核函数定理：一个对称函数$\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)$是一个合法的核函数的充要条件是，对于任意的${\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_m$，其对应的核矩阵

$$K=\left[\begin{array}{cccc}\kappa ({\mathbf{x}}_1,{\mathbf{x}}_1)& \kappa ({\mathbf{x}}_1,{\mathbf{x}}_2)& \cdots & \kappa ({\mathbf{x}}_1,{\mathbf{x}}_m)\\ \kappa ({\mathbf{x}}_2,{\mathbf{x}}_1)& \kappa ({\mathbf{x}}_2,{\mathbf{x}}_2)& \cdots & \kappa ({\mathbf{x}}_2,{\mathbf{x}}_m)\\ ⋮& ⋮& \ddots & ⋮\\ \kappa ({\mathbf{x}}_m,{\mathbf{x}}_1)& \kappa ({\mathbf{x}}_m,{\mathbf{x}}_2)& \cdots & \kappa ({\mathbf{x}}_m,{\mathbf{x}}_m)\end{array}\right]$$

是半正定的。 该定理表明，只要一个对称函数所对应的核矩阵是半正定的，那么这个函数就是一个合法的核函数。事实上，对于一个半正定核矩阵，总能够找到一个与之对应的映射$\varphi$。换言之，任何一个函数都隐式定义了一个“再生核希尔伯特空间”(RKHS)的特征空间。

• 常用的核函数有：

  1. 线性核函数：$\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)={\mathbf{x}}_i^T{\mathbf{x}}_j$

  2. 多项式核函数：$\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)=({\mathbf{x}}_i^T{\mathbf{x}}_j{)}^d$，$d\ge 1$为多项式的次数

  3. 高斯核函数：$\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)=\exp (-\frac{{\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert }^2}{2{\sigma }^2})$ $\sigma >0$为高斯核的带宽。

  4. Sigmoid核函数：$\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)=\tanh (\alpha {\mathbf{x}}_i^T{\mathbf{x}}_j+c)$ $\beta >0,\theta <0$

  5. 拉普拉斯核：$\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)=\exp (-\frac{\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert }{\sigma })$ $\sigma >0$

  6. 此外，还可以通过函数组合得到。

     1. 线性组合：$\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)=\sum _{i=1}^N{\alpha }_i{\kappa }_i({\mathbf{x}}_i,{\mathbf{x}}_j)$
     2. 核函数的直积：${\kappa }_1\otimes {\kappa }_2({\mathbf{x}}_i,{\mathbf{x}}_j)={\kappa }_1({\mathbf{x}}_i,{\mathbf{x}}_j){\kappa }_2({\mathbf{x}}_i,{\mathbf{x}}_j)$
     3. 若$\kappa (\mathbf{x},\mathbf{z})$为核函数，则$\kappa (\mathbf{x},\mathbf{z})=g(x){\kappa }_1(\mathbf{x},\mathbf{z})g(\mathbf{z})$也是核函数。

6.4 软间隔与正则化

1. 前面的讨论中，我们主要解决了两个问题：当数据线性可分时，直接使用最大间隔的超平面划分；当数据线性不可分时，则通过核函数将数据映射到高维特征空间，使之线性可分。
2. 然而在现实问题中，对于某些情形还是很难处理，例如数据中有噪声的情形，噪声数据（outlier）本身就偏离了正常位置，但是在前面的SVM模型中，我们要求所有的样本数据都必须满足约束，如果不要这些噪声数据还好，当加入这些outlier后导致划分超平面被挤歪了。

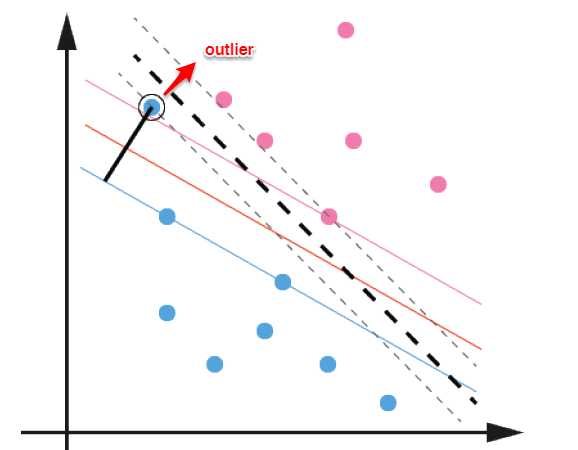
软间隔

1. 缓解该问题的一个办法是允许支持向量机在一些样本上出错。为此，要引入 “软间隔”(soft margin)的概念：

   1. 允许某些数据点不满足约束$y(w^{\prime }x+b)\ge 1$；
   2. 同时又使得不满足约束的样本尽可能少。

于是，优化目标变为：

$$\underset{\mathbf{w},b}{min}\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+C\sum _{i=1}^m{\text{loss}}_{0/1}(y_i({\mathbf{w}}^T{\mathbf{x}}_{\mathbf{i}}+b)-1)$$

其中，${\text{loss}}_{0/1}(z)$是0/1损失函数，当z小于0时，${\text{loss}}_{0/1}(z)=1$，否则为0。

2. 替代损失：然而，上述的损失函数的数学性质不佳。（非凸、非连续），人们使用其他的一些函数来代替上述函数，称为替代损失。替代损失函数一般都有较好的数学性质。以下是常用的替代损失函数：

• hinge 损失：

$$l_{\text{hinge}}(z)=max(0,1-z)$$

• 指数损失：

$$l_{\text{exp}}(z)=e^{-z}$$

• 对率损失：

$$l_{\text{log}}(z)=\log (1+\exp (-z))$$

3. 在支持向量机中，我们所使用的是hinge损失函数。引入松弛变量，则目标函数和约束条件可以改写为

$$\underset{\mathbf{w},b,\xi }{min}\frac{1}{2}\Vert w{\Vert }^2+C\sum _{i=1}^m{\xi }_i$$$$\text{s.t.}{y}_i({\mathbf{w}}^T{\mathbf{x}}_i)+b\ge 1-{\xi }_i,{\xi }_i\ge 0$$

这就是常用的软间隔支持向量机。

1. 这仍然是一个二次规划的问题。类似上述内容，我们通过拉格朗日乘数法得到对应的拉格朗日函数：

$$L(\mathbf{w},b,\xi ,\alpha ,\mu )=\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+C\sum _{i=1}^m{\xi }_i-\sum _{i=1}^m{\alpha }_i[1-{\xi }_i-y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)]-\sum _{i=1}^m{\mu }_i{\xi }_i$$

其中，${\alpha }_i\ge 0,{\mu }_i\ge 0$是拉格朗日乘数。 令${\displaystyle \frac{\partial L}{\partial \mathbf{w}}}=0,{\displaystyle \frac{\partial L}{\partial b}}=0,{\displaystyle \frac{\partial L}{\partial {\xi }_i}}=0$，得到

$$\mathbf{w}=\sum _{i=1}^m{\alpha }_i{y}_i{\mathbf{x}}_i$$$$\sum _{i=1}^m{\alpha }_i{y}_i=0$$$$C={\alpha }_i+{\mu }_i$$

代入拉格朗日函数，得到对偶问题：

$$\underset{\alpha }{max}\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_i^T{\mathbf{x}}_j$$$$\text{s.t.}\sum _{i=1}^m{\alpha }_i{y}_i=0,0\le {\alpha }_i\le C$$

这是一个凸二次规划问题，可以通过现有的优化算法求解。

1. 对于软间隔支持向量机，KKT条件为：

$$\{\begin{array}{l}{\alpha }_i\ge 0,{\mu }_i\ge 0\\ {\alpha }_i(y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)-1+{\xi }_i)=0\\ {\xi }_i>0,{\mu }_i{\xi }_i=0\\ y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)-1+{\xi }_i\ge 0\end{array}$$

于是，对任意训练样本，总有${\alpha }_i=0$或$y_{i}f(x_i)=1-{\xi }_i$，即只有支持向量对应的拉格朗日乘数不为0。由此可以看出，软间隔支持向量机的决策函数仍然是由支持向量决定的。

正则化

问题：是否可以使用其他的损失函数来替代呢？

1. 以使用对率损失为例，我们可以得到对应的优化目标：

$$\underset{\mathbf{w},b}{min}\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+C\sum _{i=1}^m\log (1+\exp (-y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)))$$

这是一个非凸优化问题，一般使用梯度下降等方法求解。 对率回归的优势主要在于其输出具有自然的概率意义，而支持向量机的输出是一个符号。此外，对率回归能直接用于多分类问题，而支持向量机需要进行一些变换。但是，对率损失是光滑的单调递减函数，不能导出类似支持向量的概念，因此对率回归的解依赖于更多的训练样本，其预测开销也更大。

1. 正则化：我们可以用更一般的形式来表示支持向量机的优化目标：

$$\underset{f}{min}\mathrm{\Omega }(f)+C\sum _{i=1}^m\text{loss}(f({\mathbf{x}}_i),y_i)$$

其中，$\mathrm{\Omega }(f)$是结构风险，第二项是“经验风险”，描述模型和训练数据之间的契合程度。而C是一个调节参数，用来平衡两者之间的关系。这种形式的优化目标称为正则化。

1. $L_p$范数正则化：它是常用的正则化项，其中，$L_1$范数正则化可以使得模型更稀疏，$L_2$范数正则化可以使得模型更平滑。$L_1$范数正则化可以用于特征选择，$L_2$范数正则化可以用于防止过拟合。

6.5 支持向量回归

现在我们来看看支持向量机的回归版本，支持向量回归（Support Vector Regression，SVR）。SVR是SVM的一个应用，用于回归问题。SVR的目标是找到一个函数f(x)使得预测值与真实值之间的误差最小。

对于回归问题，给定训练数据 $D=\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m)\}$ ，希望学得一个回归模型 $f(x)=w^{T}x+b$ 使得 $f(x)$ 与$y$尽可能接近，w和b是模型参数。

对样本 $(x,y)$ 传统回归模型通常直接基于模型输出 $f(x)$ 与真实输出y之间的差别来计算损失，当且仅当$f(x)$ 与y完全一样时，损失才为0。与此不同，支持向量回归（SVR）假设我们能容忍$f(x)$与$y$之间最多有$ϵ$的误差，仅当f(x)与y之间的差的绝对值大于$ϵ$时才计算损失。

于是，SVR问题为：（此处已经引入松弛变量${\xi }_i,{\xi }_i^{\ast }$）

$$\begin{array}{rl}\underset{w,b,\xi ,{\xi }^{\ast }}{min}& \frac{1}{2}||w|{|}^2+C\sum _{i=1}^m({\xi }_i+{\xi }_i^{\ast })\\ s.t.& y_i-w^T{x}_i-b\le ϵ+{\xi }_i\\ & w^T{x}_i+b-y_i\le ϵ+{\xi }_i^{\ast }\\ & {\xi }_i,{\xi }_i^{\ast }\ge 0\end{array}$$

引入拉格朗日乘子${\alpha }_i,{\alpha }_i^{\ast },{\mu }_i,{\mu }_i^{\ast }$，得到拉格朗日函数：（这四个值均大于等于0）

$$\begin{array}{rl}L(w,b,\xi ,{\xi }^{\ast },\alpha ,{\alpha }^{\ast },\mu ,{\mu }^{\ast })& =\frac{1}{2}||w|{|}^2+C\sum _{i=1}^m({\xi }_i+{\xi }_i^{\ast })+\sum _{i=1}^m{\alpha }_i(f(x_i)-y_i-ϵ-{\xi }_i^{\ast })\\ & +\sum _{i=1}^m{\alpha }_i^{\ast }(y_i-f(x_i)-ϵ-{\xi }_i^{\ast })-\sum _{i=1}^m{\mu }_i{\xi }_i-\sum _{i=1}^m{\mu }_i^{\ast }{\xi }_i^{\ast }\end{array}$$

后求偏导数，得到：

$$\begin{array}{rl}\frac{\partial L}{\partial w}& =w-\sum _{i=1}^m({\alpha }_i-{\alpha }_i^{\ast })x_i=0\\ \frac{\partial L}{\partial b}& =\sum _{i=1}^m({\alpha }_i-{\alpha }_i^{\ast })=0\\ \frac{\partial L}{\partial {\xi }_i}& =C-{\alpha }_i-{\mu }_i=0\\ \frac{\partial L}{\partial {\xi }_i^{\ast }}& =C-{\alpha }_i^{\ast }-{\mu }_i^{\ast }=0\end{array}$$

代入并整理，得到SVR的对偶问题：

$$\begin{array}{rl}\underset{\alpha ,{\alpha }^{\ast }}{max}& \sum _{i=1}^m{y}_i({\alpha }_i^{\ast }-{\alpha }_i)-\sum _{i=1}^mϵ({\alpha }_i+{\alpha }_i^{\ast })-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m({\alpha }_i^{\ast }-{\alpha }_i)({\alpha }_j^{\ast }-{\alpha }_j)x_i^T{x}_j\\ s.t.& \sum _{i=1}^m({\alpha }_i-{\alpha }_i^{\ast })=0,0\le {\alpha }_i,{\alpha }_i^{\ast }\le C\end{array}$$

KKT条件为：

$$\{\begin{array}{l}{\alpha }_i(ϵ+{\xi }_i-y_i+w^T{x}_i+b)=0\\ {\alpha }_i^{\ast }(ϵ+{\xi }_i^{\ast }+y_i-w^T{x}_i-b)=0\\ {\mu }_i{\xi }_i=0\\ {\mu }_i^{\ast }{\xi }_i^{\ast }=0\\ {\alpha }_i,{\alpha }_i^{\ast }\in [0,C]\\ {\mu }_i,{\mu }_i^{\ast }\ge 0\end{array}$$

SVR的解如下：

$$f(x)=\sum _{i=1}^m({\alpha }_i^{\ast }-{\alpha }_i)x_i^{T}x+b$$

其中${\alpha }_i,{\alpha }_i^{\ast }$是拉格朗日乘子，满足KKT条件。

SVR的优化问题与SVM的优化问题类似，但是SVR的目标是最小化预测值与真实值之间的误差，而SVM的目标是最大化分类间隔。

实践中，我们采用更加鲁棒的方法：选取多个或所有满足条件${\alpha }_i$的样本求解b后取平均值。

同样也可以引入核技巧，把$x$用$\varphi (x)$来代替。得到的最终的模型是：

$$f(x)=\sum _{i=1}^m({\alpha }_i^{\ast }-{\alpha }_i)K(x_i,x)+b$$

其中$K(x_i,x)$是核函数。

6.6 核方法

1. 回顾前文可以发现，若给定训练样本$\{(x_i,y_i)\}$，且不考虑偏移项b，则无论是SVM还是SVR，学得得模型总能表示成核函数$\kappa (x,x_i)$的线性组合。不仅如此，事实上，我们有一个更一般的结论：
2. 表示定理：令$\mathbb{H}$为核函数$\kappa$对应的再生核希尔伯特空间，$\Vert h{\Vert }_{\mathbb{H}}$表示$\mathbb{H}$空间中关于h的范数，$\mathbb{H}$中的任意函数$f(x)$都可以表示成核函数$\kappa (x,x_i)$的线性组合，即：

$$f(x)=\sum _{i=1}^m{\alpha }_i\kappa (x,x_i)$$

其中${\alpha }_i$是$\mathbb{H}$空间中的系数。

1. 表示定理对损失函数没有限制，对正则化项$\mathrm{\Omega }$仅要求单调递增，甚至不要求其是凸函数，意味着对于一般的损失函数和正则化项，优化问题的最优解都可以表示为核函数$\kappa (x,x_i)$的线性组合；这显示出核函数的巨大威力。
2. 核方法：核方法是指通过核函数将输入空间映射到一个更高维的特征空间，从而使得原本线性不可分的问题在新的特征空间中变得线性可分。核方法的基本思想是利用核函数$\kappa (x,x_i)$来隐式地定义一个高维特征空间，而不需要显式地计算出映射后的特征向量，从而避免了维度灾难问题。
3. 核线性判别分析：核线性判别分析（Kernel Linear Discriminant Analysis，KLDA）是核方法的一个典型应用。KLDA是线性判别分析（LDA）的核化扩展，通过核函数将输入空间映射到一个更高维的特征空间，从而使得原本线性不可分的问题在新的特征空间中变得线性可分。