Information Representation

1 Numerical Data

1. Discrete Data Values: are often used in domains like counting processes (e.g., counting) and algorithmic steps. It is applied in the representation of data that can be counted and is often represented by integers. For example, the number of students in a class, the number of books in a library, and the number of cars in a parking lot. Fixed-integers are used to represent them.

2. Continuous Data Values: are often used in domains like measurement processes (e.g., measuring) and algorithmic processes. It is applied in the representation of data that can be measured and is often represented by real numbers. For example, the height of a person, the weight of an object, and the temperature of a room. Floating-point numbers are used to represent them.

3. Finite Precision: Unfortunatly, computers can't represent real numbers with infinite precision. They can only represent them with a finite precision. To put in other words, when the FPN exceeds certain precision, the computer will be forced to lose its precision. This is known as the round-off error.

2 IEEE 754 Standard

1. Definition: The IEEE 754 standard is a widely used standard for representing floating-point numbers in computers. It defines the format of floating-point numbers, the rules for arithmetic operations, and the handling of special values like infinity and NaN (Not a Number).

   

2. Basic Components: The IEEE 754 standard defines two basic components for representing floating-point numbers: the sign bit, the exponent, and the mantissa (aka. fraction or significand). The sign bit represents the sign of the number (positive or negative), the exponent represents the scale of the number, and the mantissa represents the precision of the number.

   1. Sign Bit: It is used to represent the sign of the number. It is 0 for positive numbers and 1 for negative numbers.
   2. Exponent: It represents the scale of the number. Its value is the power of 2 by which the mantissa should be multiplied. (Notice that the exponent could be negative, which means that the number is less than 1).
   3. Mantissa: It represents the precision of the number. It is a fractional number between 1 and 2. It is a binary number.
   4. Value: The value of a floating-point number is calculated as follows.
   $$\text{Value}=(-1{)}^{\text{sign}}\times 2^{\text{exponent}}\times \text{mantissa}$$

3. Digits: The IEEE 754 standard defines several formats for representing floating-point numbers with different precisions. For a 32-bit floating-point number, the IEEE 754 standard defines 1 sign bit, 8 exponent bits, and 23 mantissa bits. For a 64-bit floating-point number, the IEEE 754 standard defines 1 sign bit, 11 exponent bits, and 52 mantissa bits.

4. Significand: Since it is limited to 23 bits, there is a finite precision to store limited digits for decimal Floating-Point Numbers.

   Computation

   For binary system, $n$ digits leads to $2^n$ unique values.

   For decimal system, $m$ digits leads to ${10}^m$ unique values.

   Then, set $2^n={10}^m$ and solve for $m$. $m=n\times {\log }_{10}2$.

   In IEEE 754,

   The 32-bit floating-point number has 23 bits for the mantissa. Then, $m=(1+23)\times {\log }_{10}2=7.22\approx 7$.

   The 64-bit floating-point number has 52 bits for the mantissa. Then, $m=(1+52)\times {\log }_{10}2=15.95\approx 16$.

5. Magnitude: For a 64-bit floating-point number, the minimum positive value that can be represented is $2.22507\times {10}^{-308}$, and the maximum positive value that can be represented is $1.79769\times {10}^{308}$.

3 Tensor

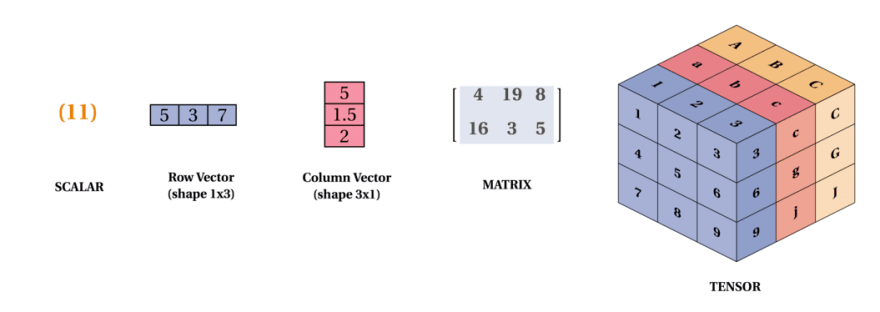
1. Definition: A tensor is a generalization of vectors and matrices to potentially higher dimensions. In fact, tensor is a multi-dimensional array, which aims to create higher-dimensional data structures (matrices, vectors, scalars).
2. Attributes: A tensor has several attributes, including the rank, the shape, and the data type.
   1. Rank: The rank of a tensor is the number of dimensions it has. For example, a scalar has a rank of 0, a vector has a rank of 1, a matrix has a rank of 2, and a 3-D tensor has a rank of 3.
   2. Shape: The shape of a tensor is the size of each dimension it has. For example, a scalar has a shape of [], a vector has a shape of [n], a matrix has a shape of [m, n], and a 3-D tensor has a shape of [m, n, p].
   3. Data Type: The data type of a tensor is the type of data it stores. For example, a tensor can store integers, floating-point numbers, or strings.

Question

Does a rank $n$ tensor define that my data dimensionality is also $n$?

No, the rank of a tensor is the number of dimensions it has, not the dimensionality of the data it represents. For example, a vector is a rank 1 tensor, but it can represent data in 1D, 2D, or 3D space, which is to say that the dimensionality of the data is (1), (2), or (3), respectively.

4 Non-Numerical Data

Notice that not all non-numerical data needs to be converted into numerical format.

1. Categorical Data: are often used in domains like classification processes (e.g., classifying) and algorithmic processes. It is applied in the representation of data that can be classified into categories and is often represented by strings.

2. Ordinal Data: are often used in domains like ranking processes (e.g., ranking) and algorithmic processes. It is applied in the representation of data that can be ordered and is often represented by integers. For example, the ranking of students in a class.

3. Image/Video Data: are often used in domains like computer vision processes (e.g., recognizing) and algorithmic processes. It is applied in the representation of data that can be visualized and is often represented by pixels.

4. Way to Represent:

   1. Convert the non-numerical data into numerical format.
   2. Embed the data into tensor structure.
   3. Perform tensor operations for further analysis.

5. One-Hot Encoding: is a common technique used to convert categorical data into numerical format. It represents each category as a binary vector, where each element corresponds to a category and is set to 1 if the category matches the element and 0 otherwise.

6. Label encoding: is another technique used to convert categorical data into numerical format. It represents each category as an unique integer value, where each integer corresponds to a category.

Question

What are their advantages? How to choose between them?

Advantages of One-Hot Encoding:

1. No ordinal assumptions: One-hot encoding does not impose any ordinal (order-related) relationships between the categories. This is particularly useful for nominal data, where categories are unordered, such as colors, countries, or gender.
2. Compatibility with many models: Models like linear regression, logistic regression, and neural networks often work better with one-hot encoded data because it avoids unintended numerical relationships between categories.
3. Interpretable: One-hot encoding creates binary features that are easy to interpret (each feature corresponds to a specific category).

Advantages of Label Encoding:

1. Efficient: Label encoding assigns a unique integer to each category, which is computationally more efficient and memory-friendly, especially when there are many unique categories.
2. Works well with tree-based models: Algorithms like decision trees, random forests, or gradient boosting can use label-encoded data effectively because they split based on feature values and don’t assume any ordinal relationships.
3. Simple to implement: Label encoding is straightforward and quick to perform.

How to choose?

1. Type of Data:

• Nominal Data (no order): Use One-Hot Encoding to avoid implying false relationships.
• Ordinal Data (ordered categories): Use Label Encoding to preserve the natural order.

2. Model Type:

• Linear Models (e.g., linear regression, logistic regression): Use One-Hot Encoding because they assume linear relationships between features.
• Tree-Based Models (e.g., decision trees, random forests, XGBoost): Use Label Encoding, as these models handle categorical data effectively and are not misled by numeric representations.
• Neural Networks: Prefer One-Hot Encoding, as it provides clearer input representations.

3. Number of Categories:

• If there are few categories, one-hot encoding is feasible.
• If there are many categories, label encoding is more efficient to prevent high-dimensional data.

4. Memory and Performance Constraints:

• High-Dimensional Data: Prefer Label Encoding for efficiency.
• Low-Dimensional Data: One-hot encoding works well.

5 Image Data

1. Image data is a 2-D grid filled with values. We have a 2-D coordinate system (Height × Width). And the numerical values $I(x,y)$ forms a pixel.
2. Notice that it could be a vector, since there is also have a third dimension, which is Channel. Channel has 3 components, R, G, B. Sometimes, componentsalpha is introduced, since transparency is considered. Its value falls in $[0,255]$.
3. For a grayscale image, at each location $(x,y)$, the pixel value $I_{(x,y)}$ is a scalar. In this case, the whole image is a 2-D tensor with ${\mathit{I}}_{(x,y)}\in {\mathbb{R}}^{h\times w\times 1}$.
4. For a RGB image, at each location $(x,y)$, the pixel value $I_{(x,y)}$ is a vector. In this case, the whole image is a 3-D tensor with ${\mathit{I}}_{(x,y)}\in {\mathbb{R}}^{h\times w\times 3}$.

Question

For a colored image, when viewed from the perspective of the channel dimension,

1. How many 2-D maps do we have?
2. Each map represents what information?

1. A colored image typically has 3 channels in the RGB format: Red, Green, and Blue. Thus, there are 3 separate 2-D maps (2-D arrays), one for each channel.
2. Each map represents the intensity values of the corresponding color channel at each pixel location.

5. For video data, it is a sequence of images. Each frame is an image. The video data is a 4-D tensor with ${\mathit{I}}_{(x,y,t)}\in {\mathbb{R}}^{h\times w\times c\times t}$.

Question

Does $n$-D means that the dimensionality of such image or video is $n$?

No, the $n$ in $n$-D tensor refers to the number of dimensions of the tensor, not the dimensionality of the data it represents. For example, a 3-D tensor can represent data in 3D space, but it can also represent data in 1D or 2D space. The dimensionality of the data is determined by the shape of the tensor, not its rank.